[UE4 PBR] Split sum appoximation 리뷰

[UE4 PBR] Split sum approximation 리뷰

최초 작성 : 2022-07-07
마지막 수정 : 2022-07-07
최재호

목차

1. 목표
2. 내용
2.1. Light equation
2.2. Diffuse BRDF
2.3. Microfacet Specular BRDF
2.3.1. Importance sampling
2.3.2. PDF and InverseCDF
2.3.3. PDF 유도
2.3.3.1 NDF(Normal Distribution function)
2.3.4. InverseCDF 유도
2.3.5. Importance sampling 을 위한 PDF 변환
2.4. 전처리 가능한 Specular part 구성
2.4.1. View = Reflect = Normal
2.4.2. Split sum approximation
2.4.3. Environment BRDF 전처리 파트에서 F0 분리
2.4.4. 분리된 근사식 코드
2.4.5. 전처리된 데이터를 사용하는 SpecularIBL 함수
3. 레퍼런스

1. 목표

Real Shading in Unreal Engine 4(레퍼런스1) 을 보고 Split sum approximation 에 대해서 알아봅시다. 이 근사 방법으로 인해서 어떻게 UE4에서 물리 기반 렌더링을 실시간으로 할 수 있게 되었는지 이해해봅시다.

2. 내용

2.1. Light equation

그림1의 식은 실제 스크린 픽셀을 평가하는 방정식입니다(여기서는 Emissive 는 제외함). 오늘은 이 식을 UE4에서 어떻게 사용하는지 알아보려고 합니다.

이 식은 단위면적에 입사하는 Radiance와 BRDF 의 곱을 적분한 것입니다. 그리고 그 결과는 단위 면적에서 특정 방향으로 빛이 나가는 Radiance 입니다. 그림1은 이 식을 Monte carlo method 또는 Importance sampling 으로 근사할 수 있음을 보여줍니다.

그림1. 반구 영역에서 단위면적에 입사하는 라이트 중 특정 방향(view 방향)으로 나가는 Radiance 를 계산하는 식, 이 식은 몬테카를로 방법을 통해서도 적분 가능함을 보여주고 있습니다. (출처 : 레퍼런스1)

레퍼런스2에서와 같이 BRDF 는 2 파트로 나눌 수 있습니다. Diffuse BRDF, Microfacet Specular BRDF 입니다. 새로운 식은 아래와 같습니다.

그림2. Diffuse, Specular 파트로 분리한 라이팅 방정식 (출처 : 레퍼런스4)

그림2의 식에서 Kd와 Ks 변수는 Diffuse or Specular BRDF 를 사용하는 비율입니다. 에너지 보존을 따르기 위해서 Kd + Ks = 1 입니다. Kd 값은 Ks 에 따라 정의됩니다. 즉, Specuar BRDF 에서 사용된 에너지에서 제외된 양이 Kd 에 사용됩니다(1 - Ks = Kd). 왜냐하면 빛이 표면에 입사하는 경우 Surface reflection 이 가장 먼저 일어나고 이로 인해 Specular reflectance 가 발생합니다. 그 후 남은 빛은 Subsurface 에 입사하며, Subsurface scattering 을 거쳐 다시 입사한 점으로부터 사방으로 나가는 빛이 Diffuse 가 됩니다. 그래서 Kd 는 Ks 에 따라 정해집니다.

이제 차례로 Diffuse BRDF 와 Microfacet Specular BRDF 에 대해서 알아봅시다.

2.2. Diffuse BRDF

레퍼런스1을 보면 Diffuse BRDF = Cdiff / π 로 정의됩니다. 여기서는 Diffuse BRDF 는 Lambertian surface 를 사용합니다. 이 surface는 아래와 같은 특성을 갖고 있습니다.
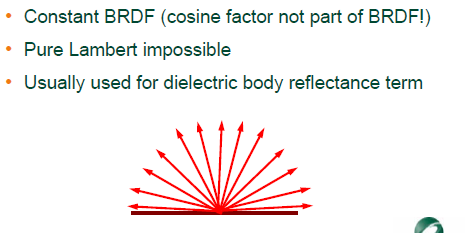
- Lambertian BRDF 의 경우 상수입니다. (Lambertian equation 에서 cosine 은 BRDF 의 파트가 아님)
- Lambertian BRDF View-Independent 입니다. 바라보는 방향이 달라진다고 밝기가 변경되지 않습니다.
-> 즉, 한 지점으로 입사한 빛(Radiance)이 다시 반구영역 중 하나로 나갈 때 어느 지점으로 나가든 동일한 양의 빛
(Radiance) 를 가집니다.

그림3. Lambertian surface 의 특성 (출처 : 레퍼런스3)

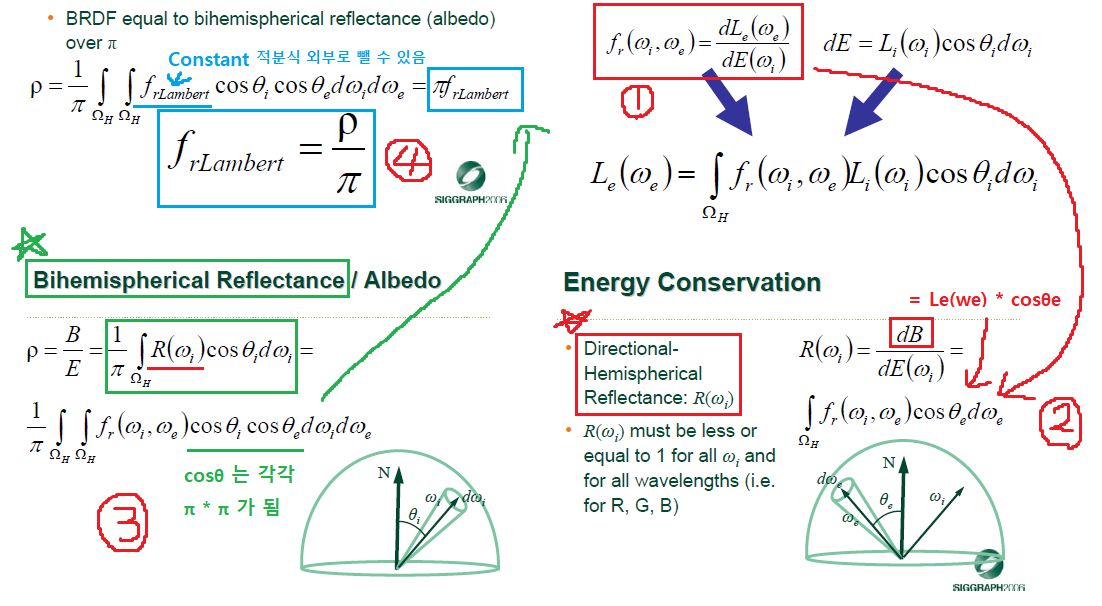
Diffuse BRDF 에서 1 / π 이 어떻게 유도되었는지 확인해봅시다. 그림4를 봐주세요.
먼저 Diffuse BRDF 를 유도하기 전에 2가지 Directional-Hemispherical Reflectance 와 Bihemispherical Reflectance 에 대해서 이해해봅시다. 이 두 가지를 이해하고 나면 Bihemispherical Reflectance는 Lambertian BRDF 이란 것을 알 수 있습니다.
먼저 Directional-Hemispherical Reflectance의 정의는 다음과 같습니다. 특정 방향에서 단위면적에 입사한 한 빛(irradiance)이 반구전체로 나가는 빛 (radiant exitance)의 비율 즉 반사율입니다. Irradiance, Raiant exitance 둘 다 특정 방향 또는 반구 전체라는 의미를 담고 있진 않습니다. 단위면적에서 들어온 에너지, 단위면적에서 나간 에너지를 뜻합니다. 특정 방향과 반구 전체는 Directional-Hemispherical Reflectance 의 정의에서부터 만들어진 것입니다.

두 번째로 Bihemispherical Reflectance 를 보겠습니다. Directional-Hemispherical Reflectance 이 특정 방향에서 입사한 빛이 반구 전체로 나가는 비율이었습니다. 하지만 실제 환경에서는 모든 방향에서부터 들어오는 빛이 모든 방향으로 반사되어 나갈 것입니다. 그것이 바로 Bihemispherical Reflectance 입니다. 또한 이것을 알베도라고 부를 수 있습니다. 알베도가 1이면 입사한 빛이 하나도 흡수되지 않고 전체가 다 반사된 것으로 볼 수 있습니다. 그림4의 3번을 보면 Directional-Hemispherical Reflectance에 대해서 반구 전체에 대해서 적분하는 것을 볼 수 있습니다. 추가로 1 / π 식이 적분식 앞에 붙어있는데요. 이 부분은 cosθ 를 반구에 대해 적분을 수행하고 나면 π가 나오기 때문에 이 부분을 normalize 하기 위해 추가된 것 입니다. 입사한 빛이 나갈 때 1 이상이 되어 에너지 보존을 깨는 부분을 막아줍니다.

마지막으로 Lambert BRDF 식을 유도해봅시다. 그림4의 4번과 같이 Lambertian BRDF = albedo / π 라는 것을 확인할 수 있습니다.

그림4. Lambert BRDF 유도 (출처 : 레퍼런스3)

여기서 BRDF의 정의를 둘러보고 가보려고 합니다. BRDF는 단위 면적에 들어오는 빛(Irradiance)에 대해 특정 방향으로 나가는 빛(Radiance)의 비율입니다(즉, Radiance / Irrdiance). 그런데 모든 방향에 대해서 동일한 양의 빛(Radiance)이 나간다면 View 방향에 따라서 BRDF의 결과가 달라지지 않을 것입니다. 그래서 상수 비율로 둘 수 있습니다. 또한 View 방향에 상관없이 BRDF 가 일정하기 때문에 BRDF는 적분식 바깥으로 빠질 수 있습니다(그림5 참고). 이러한 특성을 사용하여 우리는 Diffuse irradiance map을 전처리 할 수 있습니다. 이것은 IBL(Image-Based Lighting) 과 특정 Normal 방향을 중심으로 반구 영역 상에서 단위면적에 입사하는 모든 Radiance 를 적분한 것입니다. 이런 과정에서 Normal 방향을 Sphere 방향 전체에 대해서 미리 구해둔 것이 Diffuse irradiance map입니다. 실제 런타임에서는 적분식에서 빼낸 값들과 Diffuse irradiance map에서 샘플링한 픽셀을 곱하여 Diffuse BRDF Part 의 계산을 마칠 수 있습니다.

그림5. Light equation 에서 Diffuse 파트 (출처 : 레퍼런스 4)

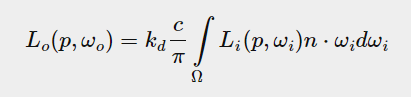
2.3. Microfacet Specular BRDF

그림6. Light equation 에서 Specular 파트 (출처 : 레퍼런스4)

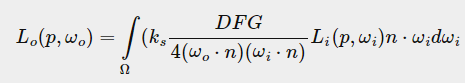
UE4에서는 Specular BRDF 로 Cook-Torrance microfacet specular shading model 을 사용합니다. Cook-Torrance 모델은 다양한 항이 있습니다. 그 항들에 어떤 함수를 사용하느냐에 따라 쉐이딩 결과가 달라질 수 있습니다. 아래 세 가지 항이 주요 항입니다.
Specular D : Distribution function 입니다. NDF(Normal distribution function)라고도 불립니다. 이 항은 주어진 방향과 일치하는 microfacet surface 분포입니다. 다양한 분포 함수가 있는데 여기서는 GGX/Trowbridge-Reitz 를 사용합니다. 식의 모양은 그림7를 참고해주세요.

그림7. GGX/Trowbridge-Reitz distribution function. a = roughness^2 (출처 : 레퍼런스1)

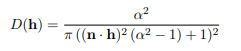
Specular F : 프레넬 항입니다. Schlick's approximation 을 사용합니다.

그림8. Schlick's approximation. F0는 Specular reflectance at normal incidence. (출처 : 레퍼런스1)

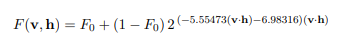
Specular G : 미세면의 Shadowing / Masking 에 대한 감쇄 함수입니다.

그림9. Schlick model 를 기반으로 몇몇 수정이 있었음. k = a / 2 로 두어서 0과 1에서 smith model 과 아주 가까워지게 함. k = a / 2 에서 a = roughness^2 인데, 이것을 ((roughness + 1) / 2)^2 으로 대체 하여 hotness를 제거함. (출처 : 레퍼런스1)

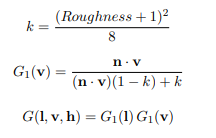
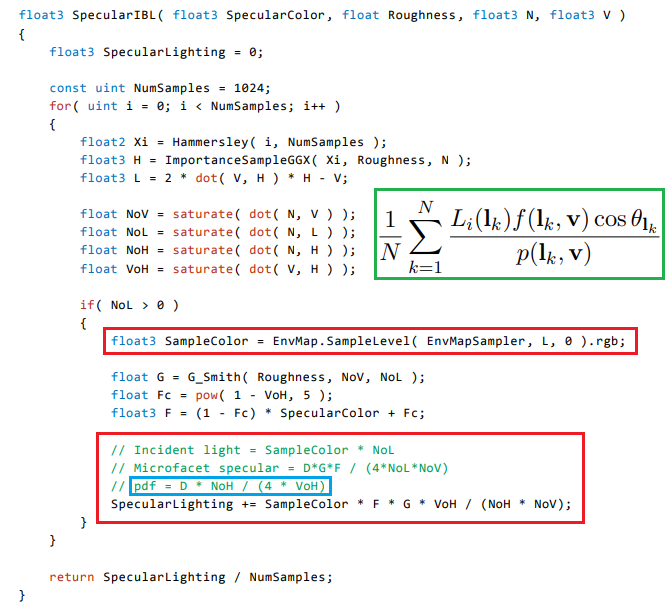
레퍼런스1에서는 Image-Based Lighting 를 사용합니다. 그림10의 SpecularIBL 함수는 IBL 로부터 입사하는 Radiance 를 Importance sampling 을 사용하여 적분합니다. 그림1의 식이 바로 그림10의 코드입니다.

그림10. Specular 파트 구현 코드, 몬테카를로 적분을 위해서 1024 개나 샘플링하고 있는 것을 볼 수 있음 (출처 : 레퍼런스1)

2.3.1. Importance sampling

그림10의 코드를 이해하기 위해서는 Importance sampling 에 대해서 이해를 하는 것이 좋습니다. 레퍼런스7 를 보면 MonteCarlo 와 Importance sampling 에 대해 알 수 있습니다. Importance sampling 를 간단히 소개하면 Numerical integration(시행횟수가 많을수록 정답에 가까워지는 적분) 이고 MonteCarlo 적분에서 정답에 더 빠르게 수렴할 수 있게 해주는 적절한 pdf를 선택한 변형입니다. 즉, 적분의 결과가 정답에 좀 더 빠르게 수렴할 수 있도록 중요도가 높은 샘플들을 이용하여 적분하는 것이 Importance sampling 입니다.

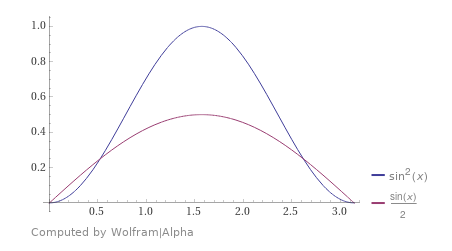
예를 들어 봅시다. 그림11 는 (sinx)^2 을 적분하는 경우, 이 함수를 적분을 위해 샘플링할 때 더 의미 있는 값(여기서는 0이 아닌 구간)을 적분을 위해 샘플링 할때 더욱 정답에 빠르게 수렴할 것입니다(이 함수를 샘플링할 때, 0 주변이나 3 주변만 주로 샘플링된다면 정답에 수렴하는데 오래 걸릴 것입니다).

그림11. Importance sampling 예제 (출처 : 레퍼런스7)

2.3.2. PDF and InverseCDF

"어떤 범위의 값이 더욱더 적분 식이 정답에 가까워지는데 중요한지?" 는 분포 함수를 통해 표현합니다. 이 분포 함수를 PDF(Probability density function) 이라고 합니다. 그림11에서는 (sinx)^2 을 적분하기 위해서 sinx / 2 를 PDF 로 사용합니다. 이 PDF는 중요한 특성이 있는데, PDF의 모든 구간을 적분하면 1이 되어야 한다는 점입니다. 발생 가능한 확률의 전체 합은 항상 100% 인 것을 생각해보면 당연합니다.

또 하나 더 알아야 하는 것은 PDF 를 적분한 CDF 입니다. 실제 사용은 InverseCDF를 사용하는데 이것은 PDF를 사용할 때, 서로 다른 PDF들의 정의역 구간을 [0, 1] 사이의 입력으로 통일시켜줍니다. 이러한 특성을 이용해서 InverseCDF 는 Uniform distribution(0~1 사이의 값들이 모두 균일한 확률을 가진 분포)으로부터 PDF 의 distribution 으로 변환하게 해줍니다. 그림12를 참고해주세요. 만약 이런과정이 없다면 정의역 범위는 0~3 또는 -pi~pi 등일 것입니다. 이 제각각의 정의역 범위에서 랜덤으로 특정 값을 샘플링 하는데는 정의역 범위도 필요할 것입니다. 만약 함수의 정의역 범위를 고려하지 않고 항상 0~1 사이의 Uniform distribution 으로 부터 PDF 의 distribution 을 얻게 해 줄 수 있다면 더 이상 PDF의 정의역의 범위를 고려하지 않아도 되며, PDF가 교체 되도더라도 기존 식에 변형을 가하지 않고도 사용 가능할 것입니다. 이 InverseCDF 함수가 그림10 의 ImportanceSampleGGX에 해당합니다.

그림12. PDF 와 CDF, InverseCDF 를 사용하여 [0,1] 사이의 랜덤 값으로 PDF 분포에 따라 값을 샘플링 할 수 있음 (출처 : 레퍼런스2)

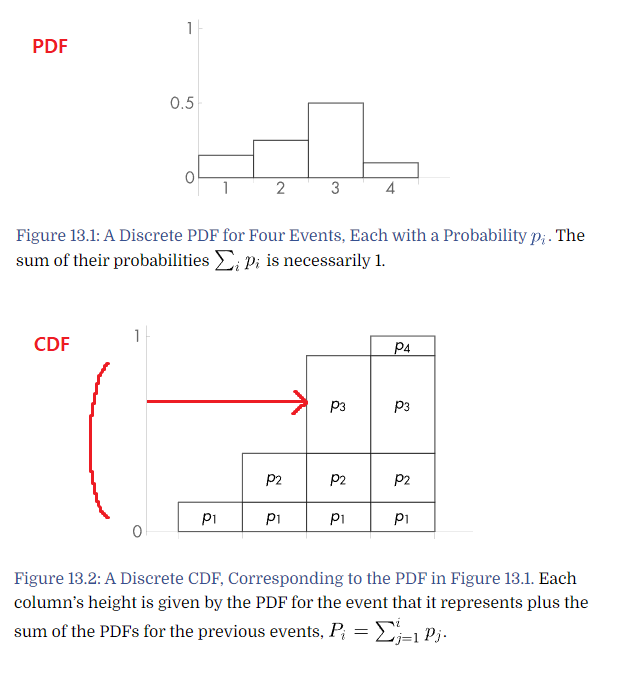
InverseCDF 함수는 D(h)로부터 유도됩니다. 그러려면 D(h)의 함수에 대해서 조금 더 이야기해보는 게 좋을 것 같습니다. D(h) 함수는 특정 방향을 향하는 미세면의 분포를 나타낸다고 했었습니다. 만약 이 미세면이 거울과 같이 macro surface normal과 완전히 일치한다면 완벽히 매끈하게 반사될 것입니다. 이 말은 microfacet surface 방향 분포가 특정 방향(macro surface normal)로 몰려있다는 것을 알 수 있습니다. 그리고 표면이 거친 경우 microfacet surface 방향의 분포가 여러 방향으로 퍼져있을 것입니다.

이렇게 Roughness 에 따라 half vector 가 될 수 있는 분포의 영역이 달라질 수 있습니다. 우리는 InverseCDF를 사용하여 [0, 1]의 Uniform distribution 을 넘기면 거기에 맞는 half vector 를 Roughness 가 고려된 분포 영역 내에서 돌려받으려 하는 것입니다.

계속해서 D(h)의 PDF와 InverseCDF 유도를 보겠습니다.

2.3.3. PDF 유도

그림13. PDF 유도 공식 (출처 : 레퍼런스 5)

2.3.3.1 NDF(Normal Distribution function)

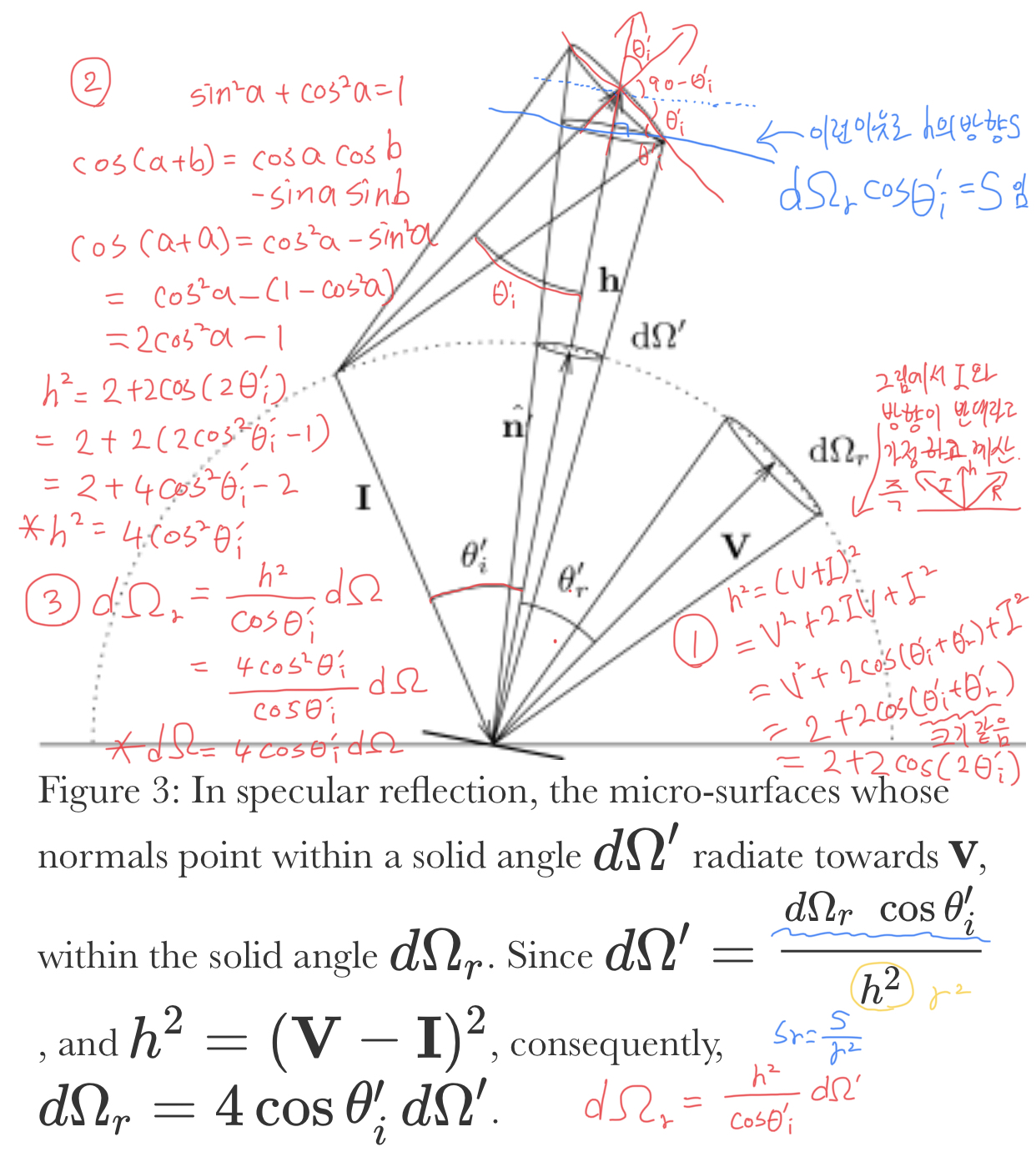
먼저 그림13에서 D(h)로부터 PDF(w) 를 유도하는 부분을 보겠습니다. D(h) * cosθ = PDF(w) 입니다. PDF 를 적분하는 경우 1이 돼야 하기 때문에 cosθ 는 노멀라이즈 텀이라 볼 수 있습니다. cosθ 를 곱해주는 것을 또 다른 측면에서 보면 D(h)는 macro surface의 단위면적당 방향 h로 향하는 macrofacet surface 의 분포로 만들기 위해서 macrofacet surface 를 macro surface 에 프로젝션 시킨것입니다. 왜냐하면 빛이 입사하는 기준은 macro surface 의 표면적을 기준으로 하기 때문입니다.

그림14. Distribution function normalize (출처 : 레퍼런스2)

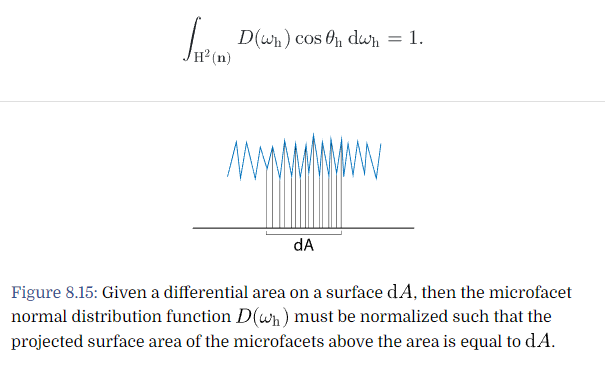
계속해서 방금 전 과정에서 구한 PDF(w)를 구면좌표계로 변환시키는 부분을 봅시다. PDF(w) * sinθ = PDF(θ,π) 인 것을 확인할 수 있습니다. 이 부분은 구면좌표계의 단위면적이 아래의 식과 같이 정의되기 때문입니다. r 은 반지름인데 단위 구라고 가정하므로 1이 되며, sinθ 만 추가되게 됩니다.

그림15. 구면좌표계로 변환 시 단위면적 (출처 : https://ko.wikipedia.org/wiki/%EA%B5%AC%EB%A9%B4%EC%A2%8C%ED%91%9C%EA%B3%84)

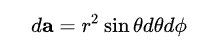
2.3.4. InverseCDF 유도

이제 CDF와 InverseCDF를 만들 차례입니다.

그림17는 PDF로부터 InverseCDF를 유도하는 과정입니다. 그리고 유도된 InverseCDF 가 ImportanceSampleGGX 함수에서 사용되는 것을 볼 수있습니다(그림17의 빨간 네모 부분). 그림17의 파란색 네모 부분은 구면좌표계의 Φ 에 해당합니다. Φ = 2 * PI * Xi.x 부분을 볼 수 있는데, 구면좌표계에서 Φ 의 범위는 [0, 2PI] 사이의 값입니다. 그렇다면 Xi.x 값의 범위는 [0, 1] 값이라는 것을 알 수 있습니다.

추가로 고려할 점이 UE4의 PBR 에서 사용하는 이 D(h) 함수는 등방성(Isotropic) 함수라서 Φ 값에 따라 분포가 바뀌진 않을 것입니다. 그래서 이 랜덤 값은 [0, 1] 사이에만 있으면 되며 어떤 값이 되던지 상관없습니다.

그림16. D(h) Isotropic 함수라 cos(theta);에만 영향을 받음. 실제 D(h) 식을봐도 cos(theta) 만 있는 것을 알 수있습니다. Anisotropic 함수의 경우 별도로 정의되어 있습니다.

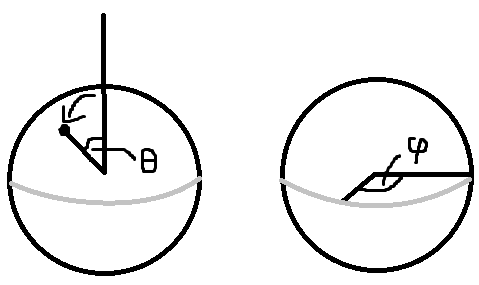
그다음으로 그림17의 빨간색 네모 부분을 봅시다. InverseCDF 는 θ 를 돌려줍니다. InverseCDF 는 입력으로 Uniform Distribution 인 [0~1] 사이의 랜덤 값을 받는다고 했습니다. 그렇다면 Xi.y 는 [0~1] 사이의 값일 것입니다.

ImportanceSampleGGX 입력값에 대해서 정리해보면 다음과 같습니다.
- Xi.x와 Xi.y 값은 Uniform distribution 랜덤 생성 함수를 통해서 0~1 사이를 값이 생성
- InverseCDF 를 통해서 분포에 맞는 half vector 에 대한 cosθ, sinθ를 얻음 (그림17의 빨간색 네모)
- 구면좌표계를 x, y, z 좌표계로 변경하여 half vector 로 변환 (그림17의 초록색 네모)

그림17. InverseCDF 생성 및 ImportanceSampleGGX 함수 분석(출처 : 레퍼런스1)

추가그림1. PDF 로 부터 CDF, InverseCDF 유도

계속해서 SpecularIBL 함수를 확인해봅시다. 그림18를 봐주세요. 여기서 초록색 네모 식을 수행하는 것이 바로 Specular IBL 함수입니다.

바로 전 확인한 함수인 ImportanceSampleGGX 함수를 통해서 얻은 Half vector 를 샘플링한 뒤 이 벡터를 통해서 필요한 식들을 생성합니다. Half vector로 유도한 Light vector를 사용하여 IBL 텍스쳐를 샘플링합니다. 그리고 초록색 네모에 있는 식처럼 SpecularLighting += L * F * cosine / pdf 를 수행하고 함수 종료 전 SpecularLighting / N 을 수행하여 최종 결과를 돌려줍니다.

SpecularLighting 구하는 중 단 하나 지금까지 설명으로 유도되지 않은 부분이 있는데, 바로 pdf 식입니다. pdf 식은 위에서 봤듯 그림18에서 보듯이 D(h) * cosθ 와 같은 모양입니다. 그런데 1 / (4 * VoH)는 어디서 나온 식일까요?

그림18. SpecularIBL 함수 분석 (출처 : 레퍼런스1)

2.3.5. Importance sampling 을 위한 PDF 변환

우리는 ImportanceSampleGGX 를 사용하여 특정 방향으로 half vector를 샘플링했습니다. 이 half vector 는 D(h)의 분포에 따라 선택되었습니다. 하지만 실제로 적분에서는 특정 방향에서 입사하는 라이트 방향에 대해서 IBL를 샘플링합니다. 즉, 실제 적분에서 사용하는 PDF는 라이트 방향이 기준이 되어야 한다는 뜻입니다. 우리는 half vector와 view vector를 통해 light vector를 유도할 수 있습니다. 비슷하게 half vector 에 대한 이런 분포 영역인 PDF 또한 half vector에서 light vector 기준으로 변환 가능합니다. 그림18은 이런 부분을 유도한 것입니다.

그림18. Half vector의 PDF로 부터 Light vector 에 대한 PDF 유도 (출처 : 레퍼런스6)

지금까지 Importance Sampling 을 적용하여 Specular 파트 적분이 더 빠르게 수렴하도록 한 부분을 같이 살펴봤습니다. 하지만 여전히 실시간으로 이 것들을 처리하기에는 계산량이 너무 많습니다. 왜냐하면 적분 식이 여전히 그대로 남아있기 때문입니다.

2.4. 전처리 가능한 Specular part 구성

지금부터는 Specular part 를 전처리 가능한 형태로 만들기 위해서 식을 수정합니다. 식을 수정하려면 Specular part의 어떤 부분이 전처리 되게 어렵게 만드는지 알아야 할 것입니다. 이 부분을 확인해 봅시다.

2.4.1. View = Reflect = Normal

Specular BRDF는 View-dependent BRDF 입니다. 그래서 BRDF 계산에는 빛이 입사하는 방향과 출력 방향(View 방향)이 반드시 필요합니다. View 방향은 런타임에서 결정됩니다. 만약 View 방향을 미리 알지 못한다면 모든 View 방향에 대해서 Specular part 를 전처리해야 됩니다. 모든 View 방향 당 전처리를 계산하는 것은 엄청난 수의 전처리 양과 저장공간을 요구할 것입니다. (Diffuse BRDF 는 모든 출력 방향으로 동일한 값이 나가기 때문에 상수 취급되어 View 방향이 필요 없었습니다.) 이 부분을 해결하기 위해서 레퍼런스1에서는 View = Reflect = Normal 으로 가정합니다. 즉, Specular part는 항상 표면의 위에서 수직으로 내려다보는 것으로 가정합니다. 이 가정으로 인해서 우리는 View 방향을 더 이상 고려하지 않아도 됩니다. 그리고 전처리 가능하게 됩니다.

단 이 가정으로 인해서 Grazing angle에서의 Specular reflection 모양의 이점을 잃게 됩니다.

그림19. 전처리를 위해서 V = R = N 으로 설정하여 Grazing angle에서 specular reflection 의 장점을 잃어버림 (출처 : 레퍼런스4)

2.4.2. Split sum approximation

식을 더 유연하게 만들기 위해서 2가지 작업을 추가로 수행합니다. 첫 번째 작업은 Specular part 를 2개로 분리입니다. 그림20를 봐주세요. 첫번째 부분은 현재 IBL 인 환경에 대한 전처리 부분이며, 두 번째 부분은 BRDF 에 대한 전처리입니다. 분리된 식의 왼쪽은 IBL 에 대해 특정 지점으로 입사하는 라이트를 모두 적분한 식입니다. 오른쪽 식은 BRDF 를 포함한 나머지 부분입니다. 이렇게 두개로 나뉘게 되면 IBL 텍스쳐가 변경되는 경우 왼쪽의 식을 IBL에 대한 전처리만 미리 구해두면 됩니다. 그리고 BRDF 를 포함한 오른쪽 식은 한번 생성한 뒤 계속해서 재활용합니다.

레퍼런스1을 보면 분리된 식의 왼쪽은 Pre-filtered Environment Map, 오른쪽은 Environment BRDF 라고 부릅니다.

그림20. Split sum approximation (출처 : 레퍼런스1)

이렇게 식을 2개로 나뉘었기 때문에 레퍼런스1에 소개된 이름처럼 Split sum approximation 이라 부르는 것 같습니다.

2.4.3. Environment BRDF 전처리 파트에서 F0 분리

두 번째 작업은, 오른쪽 BRDF를 포함하는 식을 정리하여 머터리얼의 적용을 런타임에서 가능하도록 합니다. 그림21에서 보는 것과 같이 식을 정리하여 머터리얼의 F0 부분을 전처리 과정에 빼내서 추후 런타임에서 적용할 수 있도록 식을 변경했습니다. 레퍼런스1에서 사용하는 Schlick's approximation 프레넬 항의 경우 F0 만이 재질 특성에 영향을 주는 것을 볼 수 있습니다(그림8의 식 참고). 그래서 식을 변경하여 F0 를 적분 바깥으로 빼냅니다. 이렇게 되면 적분 내에 있는 식들만 전처리해두고, 전처리한 것들을 실제 사용할 때 F0을 곱하여 사용할 수 있습니다. 그림21의 식을 보면 BRDF 는 F 로 나눠주고 있는데 BRDF는 F 항을 포함하기 때문에 이 부분은 자연스럽게 소거될 것입니다.

그림21. 전처리 과정에서 머터리얼의 F0 값을 분리하여 실시간으로 처리하게 할 수 있게 식 변경 (출처 : 레퍼런스1)

추가그림2. F0 인자를 적분식의 외부로 분리하는 과정 유도

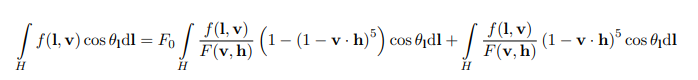
2.4.4. 분리된 근사식 코드

Pre-filtered Environment Map (분리된 식의 왼쪽 부분의 전처리)
전처리된 Pre-filtered Environment map은 Roughness 별로 텍스쳐 Mipmap에 저장되며 사용 사 Roughness를 통해 어떤 Miplevel을 사용할지 결정합니다.

그림22. Split sum approximation 으로 분리된 파트의 앞쪽 (출처 : 레퍼런스1)

Environment BRDF (분리된 식의 오른쪽 부분의 전처리)

그림23. Split sum approximation 으로 분리된 파트의 뒤쪽 (출처 : 레퍼런스1)

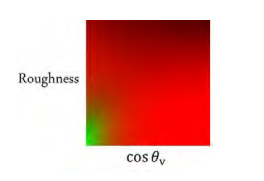
Environment BRDF 의 전처리로 생성된 LUT 는 그림24에서 볼 수 있습니다.

그림24. Environment BRDF 전처리로 생성된 LUT (출처 : 레퍼런스1)

2.4.5. 전처리된 데이터를 사용하는 SpecularIBL 함수

최종적으로 Specular Part를 계산하는 식은 그림25에서 볼 수 있습니다.

그림25. 최종적으로 만든 Specular 파트 함수 (출처 : 레퍼런스1)

그림26. 맨 위쪽이 레퍼런스, 가운데가 split sum approximation, split sum approximation 과 n = v 가정 까지 모두 포함됨. 거의 차이가 없음을 확인할 수 있음 (출처 : 레퍼런스1)

3. 레퍼런스

1. Real Shading in Unreal Engine 4
2. PBRT
3. Reflectance, Siggraph 2006, Naty
4. Learn OpenGL
5. Sampling microfacet BRDF
6. Reflectance of Polytetrafluoroethylene (PTFE) for Xenon Scintillation Light, C. Silvaa), J. Pinto da Cunha, A. Pereira, V. Chepel, M. I. Lopes, V. Solovov, and F. Neves
7. Monte Carlo Integration Explanation in 1D 번역 링크