| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- VGPR
- Wavefront
- wave
- Nanite
- unrealengine
- Shadow
- deferred
- forward
- GPU
- scalar
- vulkan
- SIMD
- UE5
- ShadowMap
- optimization
- Study
- Graphics
- DX12
- SGPR
- shader
- GPU Driven Rendering
- ue4
- hzb
- scattering
- 번역
- rendering
- RayTracing
- DirectX12
- atmospheric
- texture
- Today
- Total
RenderLog
Tangent Space, Tanget Vector 생성 본문
Normal map을 사용하기 위해서는 텍스쳐 공간에서 오브젝트 공간으로의 공간변환이 필요합니다.
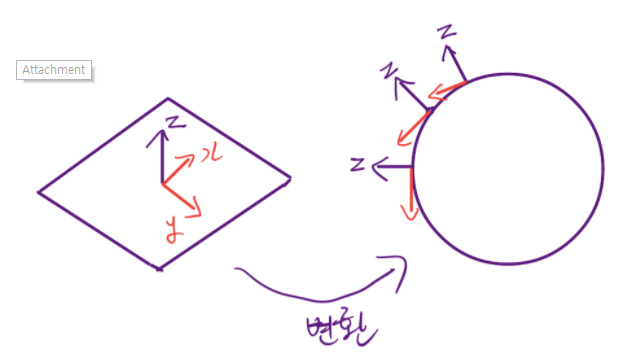
Tangent vector(접선 벡터)는 Normal에 수직인 평면에 존재하는 벡터입니다. 이 평면을 Tangent plane 이라 부릅니다. 또한 Tangent plane에 위치하면서 Tangent vector와 수직인 벡터를 Bitangent vector라고 부릅니다. (Binormal 로도 부릅니다.)
텍스쳐에 있는 Normal을 오브젝트의 표면에서 사용하려면, 텍스쳐 공간에서 오브젝트 공간으로의 공간변환이 필요합니다.
변환 방법은 아래와 같습니다.
Tangent space 로 공간변환
TBN Matrix
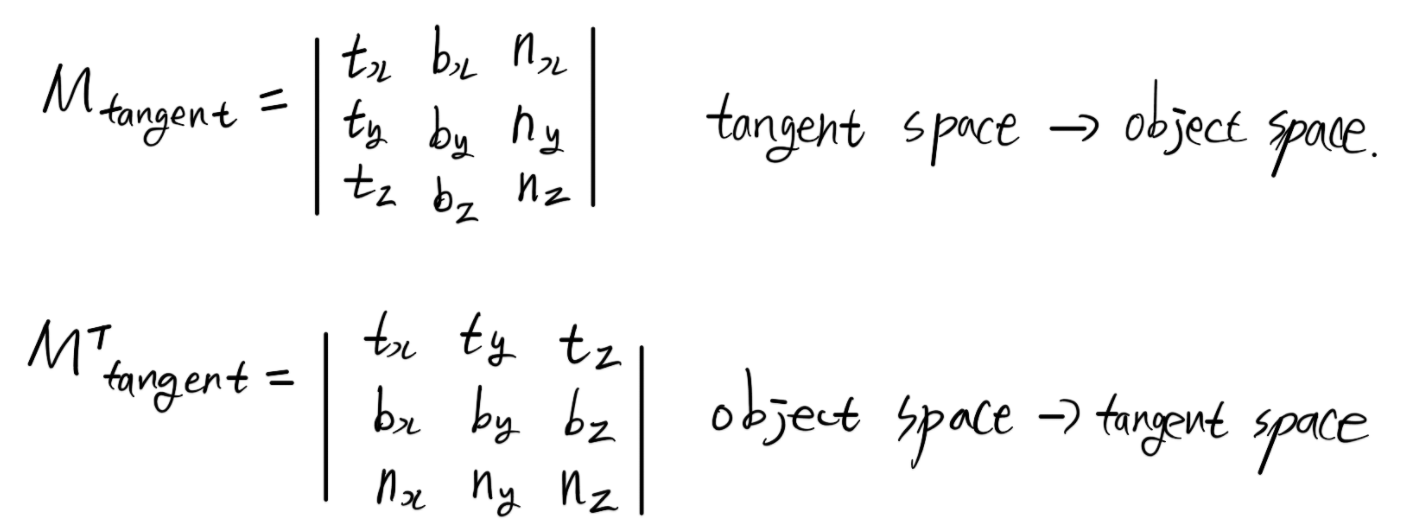
Tangent vector 생성
삼각형을 이루는 반시계 방향의 점 3개 P0, P1, P2 가 있다고 둡니다. 이 3개의 점으로 T, B 벡터를 유도할 것입니다.
아래의 그림처럼 2개의 점을 사용해 얻은 벡터를 T와 B 를 기저로 하는 벡터 공간에서 표현 할 수 있다는 점으로 T, B 벡터를 유도할 것입니다.

벡터 T와 B를 얻기 위해서 연립방정식(System of equations)를 사용합니다.

얻어진 T, B 벡터는 이 정점을 공유하고 있는 모든 삼각형들의 T, B 벡터와 합산하여 계산합니다.

여러개의 T, B 벡터를 합산하고 나면 T, B, N 벡터는 서로 수직이 아닐 수 있습니다.
그래서 아래와 같은 과정으로 수직을 만들어 줍니다. (Gram-Schmitdt orthonormalization)
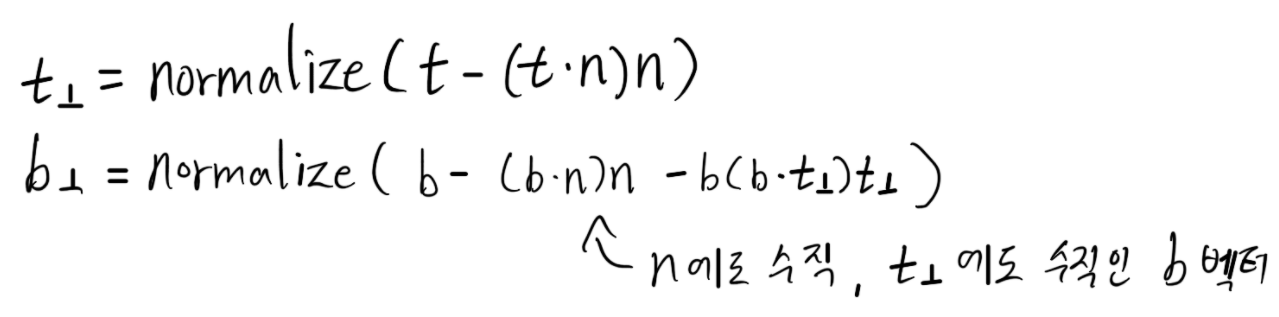
T, B, N 벡터를 모두 구하면 이제 부터는 Normal 을 탄젠트 공간에서 오브젝트 공간으로 변환 가능합니다.
공간을 절약하기 위해서 B 벡터를 저장하지 않는 경우
T, N 벡터만 있으면 B 벡터는 언제든 외적을 사용하여 생성할 수 있습니다. 그래서 T, B 벡터만 저장해도 됩니다. 이경우 한가지 더 고려해야 할 점이 있는데, 왼손 / 오른손 좌표와 관계없이 B 벡터를 생성해 내기 위해서 아래와 같은 방식으로 Bitangent vector 를 생성합니다. 그리고 왼손/오른손 좌표계 관계없이 B 벡터를 만들기 위해 추가적으로 부호 값을 저장합니다.

Source code
void CalculateTangents(Vector4* OutTangentArray, int InTriangleCount, const Triangle* InTriangleArray, int InVertexCount, const Vector3* InVertexArray, const Vector3* InNormalArray, const Vector2* InTexCoordArray)
{
// 임시버퍼 생성
Vector3* Tangent = new Vector3[InVertexCount * 2];
Vector3* Bitangent = Tangent + InVertexCount;
for (int i = 0; i < InVertexCount; ++i)
{
Tangent[i] = Vector3::ZeroVector;
Bitangent[i] = Vector3::ZeroVector;
}
// 모든 삼각형에 대해서 Tangent와 Bitangent를 계산하고 삼각형의 3개의 Vertex에 Tangent와 Bitangent를 더해줍니다.
for (int k = 0; k < InTriangleCount; ++k)
{
int i0 = InTriangleArray[k].Index[0];
int i1 = InTriangleArray[k].Index[1];
int i2 = InTriangleArray[k].Index[2];
const Vector3& p0 = InVertexArray[i0];
const Vector3& p1 = InVertexArray[i1];
const Vector3& p2 = InVertexArray[i2];
const Vector2& w0 = InTexCoordArray[i0];
const Vector2& w1 = InTexCoordArray[i1];
const Vector2& w2 = InTexCoordArray[i2];
Vector3 e1 = p1 - p0;
Vector3 e2 = p2 - p0;
float x1 = w1.x - w0.x;
float x2 = w2.x - w0.x;
float y1 = w1.y - w0.y;
float y2 = w2.y - w0.y;
float r = 1.0f / (x1 * y2 - x2 * y1);
Vector3 t = (e1 * y2 - e2 * y1) * r;
Vector3 b = (e2 * x1 - e1 * x2) * r;
Tangent[i0] += t;
Tangent[i1] += t;
Tangent[i2] += t;
Bitangent[i0] += b;
Bitangent[i1] += b;
Bitangent[i2] += b;
}
// 각각의 Tangent를 Orthonormalize 하고, Handedness 하게 계산가능하도록 w 에 부호 추가
for (int i = 0; i < InVertexCount; ++i)
{
const Vector3& t = Tangent[i];
const Vector3& b = Bitangent[i];
const Vector3& n = InNormalArray[i];
OutTangentArray[i].xyz() = Normalize(Reject(t, n)); // Normalize(t - Dot(t, n)*n)
OutTangentArray[i].w = (Dot(Cross(t, b), n) > 0.0f) ? 1.0f : -1.0f;
}
delete[] Tangent;
}
Reference
Foundations of Game Engine Development 2
'Graphics > Graphics' 카테고리의 다른 글
| Signed Distance Fields (2) | 2020.04.13 |
|---|---|
| Light Indexed Deferred Rendering (0) | 2020.04.03 |
| DeepShadowMap(DSM) (0) | 2020.02.25 |
| Dual Paraboloid ShadowMap (0) | 2020.02.18 |
| DeferredRenderingMSAA (0) | 2020.02.12 |




