Variance Shadow Map(VSM)

 

 

Variance Shadow Map(VSM)

 

최초작성 : 2020-04-16

마지막수정 : 2020-04-16

최재호

 

개요

Standard shadow map 의 Shadow edge를 부드럽게 처리할 수 있는 기법 중 하나입니다.

 

VSM은 PCF에서 발전한 알고리즘입니다. PCF는 현재 픽셀의 Depth 값과 Shadow map의 일정 영역의 Depth 값을 비교하여, Shadowing 되는 비율을 얻어내는 알고리즘입니다. 만약 비교한 Shadow map의 영역이 총 9개의 텍셀이고, 그중 3개만 Shadowing 상태면 3/9 = 1/3 만 Shadowing 처리를 하여 Shadow의 가장자리를 부드럽게 처리합니다.

 

VSM을 만든 저자는 우리가 PCF를 할때 실제로 하려고 하는것에 집중했습니다. PCF 를 진행할 영역의 Shadowing 비율만 얻을 수 있다면 된다고 생각합니다.

 

이것을 하기 위해서 체바쇼프 부등식을 사용합니다. 체바쇼프 부등식은 분산(Variance)을 사용하기 때문에 분산에 대해 먼저 알아보려 합니다. 분산에 대한 자세한 강의는 이 링크에서 잘 설명해줍니다.

 

분산은 평균으로 부터 알수 없는 정보를 얻기 위해서 생겨난 개념입니다.

예를들어 평균이 50인 학급이 2개 있다고 합니다. 학급 A는 50점, 50점 그리고 학급 B는 20점, 80점 이라고 합시다.

평균으로는 이 학급의 평균 점수가 얼마나 신뢰할 수 있을지 알수 없습니다. 그래서 분산(혹은 표준편차)을 사용하여 학급의 개개인의 점수가 평균점수와 얼마나 많이 떨어져있는지 확인합니다.

 

학급A
점수 : 20 80

제평 (400 + 6400) / 2 = 3400 
평제 ((20 + 80) / 2)^2 = 2500

분산 : 3400 - 2500 = 900

--------------------------------
학급A
점수 : 50, 50

제평 (2500 + 2500) / 2 = 2500
평제 ((50 + 50) / 2)^2 = 2500

분산 : 2500 - 2500 = 0

 

Shadow의 경계가 되는 부분을 판단하기 위해서 우리는 분산값을 사용할 수 있습니다.

위의 예제 처럼 평균점수와 각각 학생들의 점수가 동일하면 0, 차이가 있다면 0에서 점점 멀어지는 수가 됩니다.

이제 쉐도우에 이것을 적용하게 되면, 아래처럼 특정 Depth 값의 차이가 클수록 분산 값이 더 커질 것입니다.

 

특정 영역A
Depth : 0.3, 0.5

제평 (0.09 + 0.25) / 2 = 0.17 
평제 ((0.3 + 0.5) / 2)^2 = 0.16

분산 : 0.17 - 0.16 = 0.01

--------------------------------
특정 영역B
Depth : 0.3, 0.3

제평 (0.09 + 0.09) / 2 = 0.09
평제 ((0.3 + 0.3) / 2)^2 = 0.09

분산 : 0.09 - 0.09 = 0

 

이제 체바쇼프 부등식을 확인해 봅시다. VSM은 실제로 체바쇼프 부등식(Chebyshev's inequality)을 사용하여 Shadowing 여부를 결정하는 것 외에는 Standard shadow map과 큰 차이가 없습니다.

 

Chebyshev's inequality (레퍼런스1에서 가져옴)

(레퍼런스1에서 가져옴)

 

E(x) = 기대값(평균)

E(x^2) = 제곱의 기대값(평균)

t : 현재 비교하고자 하는 값 (현재 픽셀의 Depth)

여기서 시그마 기호는 표준편차를 의미하는데, 표준편차의 제곱은 분산입니다.

분산 = 제평평제 (제곱의 평균 - 평균의 제곱)

 

 

레퍼런스1에서 가져온 VSM 코드 (이상한 점은 mD를 구하는 과정에서 moments.x, fragDepth 순서가 바뀜)

 

 

위에서 예로 사용한 분산값을 체바쇼프 부등식에 사용해서 결과를 확인해보겠습니다.

특정 영역B
Depth : 0.3, 0.3

제평 (0.09 + 0.09) / 2 = 0.09
평제 ((0.3 + 0.3) / 2)^2 = 0.09

분산 : 0.09 - 0.09 = 0

이 경우는 분산값이 0이 되면서, 체바쇼프 부등식 자체가 0이 되어버립니다.
(이 경우에는 현재 픽셀의 Depth값과 Shadow map의 평균 Depth 값을 비교하여 Shadowing을 처리합니다.)

--------------------------------
아래의 경우

특정 영역A
Depth : 0.3, 0.5

제평 (0.09 + 0.25) / 2 = 0.17 
평제 ((0.3 + 0.5) / 2)^2 = 0.16

분산 : 0.17 - 0.16 = 0.01

이경우는 체바쇼프 부등식이 아래와 같을 것입니다.
0.01 / (0.01 + (0.4 - t)) = p

Depth 값 0.0, 0.4, 0.8을 차례로 대입해 보겠습니다.
Depth 0.0 : 0.02439
Depth 0.2 : 0.04761
Depth 0.4 : 1
Depth 0.8 : -0.25641

0.4 이후로는 값이 마이너가 됩니다.
(이 경우에도 현재 픽셀의 Depth값과 Shadow map의 평균 Depth 값을 비교하여 Shadowing을 처리합니다.)

 

아래와 같은 조건에서는 Shadow map의 평균값과 현재 픽셀의 Depth 값을 Shadowing에 사용합니다.

1. 분산값이 0

2. Shadow map의 평균값과 Depth 값을 비교한 결과 그림자 바깥에 있는 경우 (그냥 Lit 으로 판정)

3. 체바쇼프 방정식의 결과 값이 마이너스가 된경우

 

이렇게 체바쇼프 부등식을 사용하여 쉐도우 경계부분에서 Shadowing 값을 부드럽게 변화 시킬 수 있다는 것을 확인하였습니다.

 

VSM에도 단점있는데 바로 Light Bleeding 입니다.

아래 그림처럼 빛이 그림자 내로 새어들어가는 현상을 말합니다.

 

레퍼런스 3에서 가져온 그림

 

이 현상이 발생하는 이유는 아래와 같습니다.

광원과 가장 가까운 거리에 있는 물체의 Depth가 shadow map에 저장되면서, 아래 그림의 빨간 동그라미 부분의 Depth 차이가 발생하게 됩니다. 이렇게 되면 분산값이 커지면서 Filter region이 Shadow 의 경계라고 판단하게 됩니다.

이 부분을 해결하기 위해서 레퍼런스 3번 자료의 해결방법으로 Light bleeding 문제를 완화하였습니다. 이 부분은 VSM 구현에 핵심은 아니니 관심있으신 분은 레퍼런스 3을 참고해주세요.

 

레퍼런스 3에서 가져온 그림

 

 

이제 실제 구현 코드를 보겠습니다. 제가 구현한 코드가 있긴 하지만 Nvidia 완전한 코드를 제공하니 참고해보시면 좋을것 같습니다. 차이점으로는 제코드는 Omni directional light에도 VSM을 적용한 점 입니다.

구현 프로세스

VSM을 사용하는데 Standard Shadow Map과 달라지는 점은 딱 2군대 입니다.

1. Shadow map을 만들때 Shadow map에 Depth와 Depth*Depth를 저장합니다.

2. Shadow 판정시 체바쇼프 부등식을 사용합니다.

 

즉, Standard shadow map에서 Shader만 바뀌면 됩니다.

 

1. Generate shadow map for VSM

저의 경우 Linear Depth 값을 사용하고 싶어서 Depth를 저장하지 않고, 실제 World space에서의 거리를 사용해 계산했습니다.

 

Depth와 Depth의 제곱을 텍스쳐의 X, Y 컴포넌트에 저장

 

 

2. Blur shadow map (기대값(평균)을 계산함)

이 과정에서 Depth 값의 평균과 Depth값 제곱의 평균이 구해집니다.

필터링은 가로세로 총 2번 진행했습니다.

 

 

 

텍스쳐 범위를 벗어난 부분은 float_max 값을 Depth로 사용하여 Shadow map 테두리 부분에 발생하는 Artifacts를 제거했습니다.

 

Shadow map 테두리에서 발생할 수 있는 Artifacts

 

 

 

3. Base pass에서 Shadow map을 사용하여 그림자 그림

 

체바쇼프 부등식을 사용한 VSM 처리

 

 

구현 결과

위의 구현코드에서는 Directional Light인 경우의 VSM 코드만 보여드렸는데, 실제 구현은 Point Light(Omni directional light)에도 구현하였습니다. 그만큼 Standard shadow map과 호환성이 좋아 쉽게 사용가능합니다.

 

VSM with Directional Light

 

VSM with Directional Light

 

 

VSM with Point light

 

VSM with Point light

 

 

VSM with Spot light

 

VSM with Spot light

 

 

VSM with Directional / Point / Spot lights

 

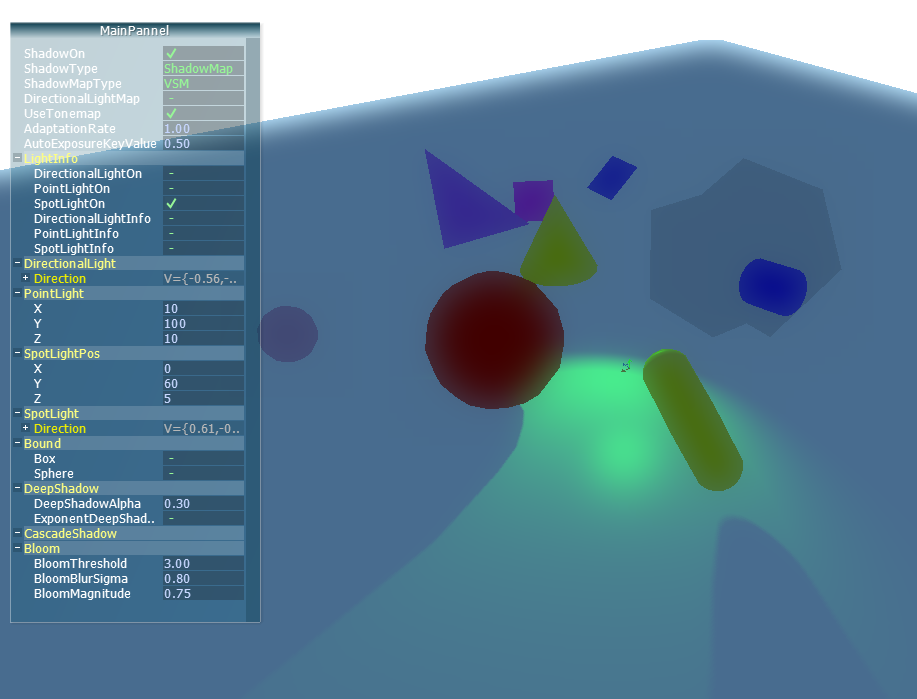
VSM with Directional / Point / Spot lights

 

 

레퍼런스

1. http://developer.download.nvidia.com/SDK/10/direct3d/Source/VarianceShadowMapping/Doc/VarianceShadowMapping.pdf

2. https://youtu.be/trFS6ug4_T4

3. https://developer.nvidia.com/gpugems/gpugems3/part-ii-light-and-shadows/chapter-8-summed-area-variance-shadow-maps