| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- atmospheric
- shader
- 번역
- optimization
- Graphics
- Study
- rendering
- texture
- SGPR
- DX12
- hzb
- scalar
- SIMD
- GPU Driven Rendering
- GPU
- deferred
- RayTracing
- vulkan
- Shadow
- ShadowMap
- scattering
- unrealengine
- Nanite
- wave
- Wavefront
- ue4
- VGPR
- UE5
- DirectX12
- forward
- Today
- Total
RenderLog
[번역] Accurate Atmospheric Scattering 본문
개인 공부용으로 번역한 거라 잘못 번역된 내용이 있을 수 있습니다.
또한 원작자의 동의 없이 올려서 언제든 글이 내려갈 수 있습니다.
출처 : https://developer.nvidia.com/gpugems/gpugems2/part-ii-shading-lighting-and-shadows/chapter-16-accurate-atmospheric-scattering
[GPU Gems2] Chapter 16. Accurate Atmospheric Scattering
Sean O'Neil
16.1 Introduction
컴퓨터 그래픽스를 위한 사실적인 대기 산란을 생성하는 것은 항상 어려운 문제였습니다, 그러나 그것은 실외 환경을 사실적으로 렌더링하는데 가장 중요합니다. 대기 산란을 설명하는 방정식들은 그 주제에 책 전체를 할애할 만큼 아주 복잡합니다. 컴퓨터 그래픽스 모델은 보통 방정식들을 간략화 합니다, 그리고 interactive frame rate 에서 실행되는 것은 거의 없습니다. 이 챕터는 Nishita et al(1993)의 방법을 사용하여 GPU에서 리얼타임 대기 산란 알고리즘을 구현하는 방법에 대해서 설명합니다. 그림 16-1은 이 책의 CD에 포함된 산란 데모의 스크린샷을 보여줍니다.

많은 대기 산란 모델들은 카메라가 항상 지면위에 있거나 지면에 가까이 있다고 가정합니다. 이것은 대기가 모든 고도에서 상수 밀도를 가지도록 가정하여 문제를 쉽게 만듭니다. 상수 밀도는 Nishita et al(1993)의 산란 방정식을 엄청나게 간략화 합니다. GPU 쉐이더에서 이러한 간략화된 방정식을 구현하는 것은 Hofman과 Preetham 2002를 참고해주세요. 이 구현은 DirectX 8.0 쉐이더에서 아주 빠른 매력적인 산란 효과를 생성합니다. 불행히도, 항상 정확한 결과를 생성하진 않습니다, 그리고 카메라가 우주 혹은 아주 지면에서 높은 위치에 위치하는 비행 혹은 우주 시뮬레이터와 잘 작동하지 않습니다.
이 챕터는 Nishita et al(1993)의 전체 방정식을 Iterative frame rates에서 작동하는 GPU Shadder로 어떻게 구현하는지에 대해 설명합니다. 이러한 방정식은 대기를 고도의 증가에 따라 지수적인 밀도의 감쇄로 더 정확하게 모델링합니다. O'Neil 2004는 CPU에서 작동하는 비슷한 알고리즘을 설명합니다, 그러나 그 알고리즘은 너무 CPU-집중적 입니다. 4개의 부동소수점을 채널로 미리계산된 2D 조회(Lookup) 테이블을 기반으로 합니다. 각각의 정점을 위한 컬러 계산은 테이블을 여러번의 조회 하는 것과 각 조회에 대해서 추가 계산이 필요했습니다. 글을 쓴 당시에, 1개의 패스의 Shader에서 GPU는 이런 연산을 지원하지 않았습니다.
이 챕터에서, 우리는 이미지 품질의 희생없이 조회 테이블을 제거하여 우리가 전체 알고리즘을 GPU Shader에서 구현할 수 있게 합니다. 이런 Shader들은 DirectX 2.0 쉐이더 모델을 지원하는 GPU에서 리얼타임으로 작동하기에 충분히 작고 빠릅니다.
16.2 Solving the Scattering Equations
산란 방정식은 분석적으로 해결이 불가능한 nested integral이 있습니다; 다행히도, 사다리꼴 법칙과 같은 기술로 수치적으로 적분 값을 쉽게 계산할 수 있습니다. 이 방법으로 적분을 근사화하는 것은 반복문에서 계산되어지는 가중합을 단순화합니다. 그래프에 선분을 상상해보세요: 선분을 n 개의 부분으로 나누고 각각의 샘플 부분의 중심점에서 적분함수를 구하세요. 각각의 결과에 샘플의 길이를 곱하고 그들을 모두 더하세요. 더 많은 샘플을 사용하는 것은 결과를 더 정확하게 합니다, 그러나 또한 적분 계산을 더 비싸게 만듭니다.
우리의 경우, 선분은 카메라로 부터 대기를 통과하고 특정 Vertex 까지의 도달하는 반직선입니다. 이 Vertex는 지형, 스카이돔, 구름 혹은 우주에 있는 달과 같은 오브젝트의 일부일 수 있습니다. 만약 반직선이 대기를 통과하여 Vertex에 도달하였다면, 산란의 계산이 필요합니다. 모든 반직선은 어디에서 반직선이 대기를 통과하기 시작했고 어디에서 대기를 통과하는 것을 멈췄는지를 표시하는 2개의 점을 가지고 있습니다. 우리는 이 점을 A와 B라고 부를 것입니다, 그리고 그들은 그림16-2에 있습니다. 카메라가 대기 내에 있을때는, A는 카메라의 위치입니다. Vertex가 대기내에 있을때, B는 Vertex의 위치입니다. 어느쪽 위치든 우주에 있다면, 우리는 광선이 외부 대기와 교차하는 곳을 찾기 위해서 Sphere-intersection을 수행합니다, 그리고나서 우리는 교차점 A 또는 B를 만듭니다.
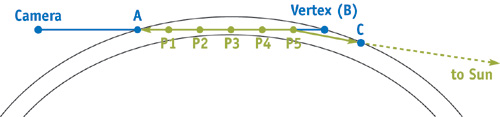
이제 우리는 2점으로 부터 정의된 선분을 가집니다, 그리고 우리는 선분의 길이에 따른 대기 산란을 나타내는 적분을 근사하고 싶습니다. 이제 5개의 샘플 위치를 잡고 그 위치들을 P1에서 P5로 이름 붙입니다. 각각의 점 P1 부터 P5는 대기 내부에서 빛이 산란되는 위치을 나타냅니다; 라이트는 태양으로부터 대기로 들어옵니다, 그 지점에서 산란합니다, 그리고 카메라쪽으로 반사됩니다. 예로 점 P5를 고려해봅시다. 태양광은 태양으로 부터 직선으로 P5로 갑니다. 이 선을 따라서 P5에서 일부 빛을 산란시킵니다. P5에서, 이 라이트의 일부가 카메라로 직접 산란됩니다. P5로 부터 라이트가 카메라로 이동할때, 라이트의 일부는 다시 산란되어집니다.
16.2.1 Rayleigh Scattering vs. Mie Scattering
또 다른 중요한 세부사항은 P 지점에서 라이트의 산란이 모델링 되는 방법과 연관되어있습니다. 대기안의 서로다른 입자들은 라이트를 서로다른 방향으로 산란시킵니다. 대기안에서의 산란 형태의 가장 일반적인 2가지는 Rayleigh 와 Mie 산란입니다. Rayleigh 산란은 공기중의 작은 분자들에의해서 발생합니다, 그리고 이 분자들은 라이트를 짧은 파장에서 더 강하게 산란시킵니다. (파랑색 먼저, 그리고나서 초록, 그리고나서 빨강). 하늘은 파랑색입니다. 왜냐하면 파랑색 라이트는 사방으로 튀기 때문입니다, 그리고 궁극적으로 모든 방향에서부터 당신의 눈에 도달합니다. 태양의 라이트는 일몰에 노랑/오랜지/레드로 바뀝니다. 왜냐하면 라이트가 대기를 통과하여 먼거리를 이동했기 때문입니다, 거의 모든 파랑과 많은 초록 라이트가 당신에게 도착하기 전에 붉은색만 남겨둔채로 산란되어집니다.
Mie 스캐터링은 Aerosols라 불리는 공기중의 큰 입자에 의해서 발생합니다 (먼지나 오염 같은), 그리고 그것은 라이트의 모든 파장을 동일하게 산란시키는 경향이 있습니다. 흐린날에, Mie 산란은 하늘을 약간 회색으로 보이게 만들고 태양의 주변에 큰 흰색의 후광(halo)를 만들게 합니다. Mie 산란은 물의 작은 입자와 공기중의 얼음으로 부터 라이트 산란을 시뮬레이션 하는데 사용되어질 수도 있습니다, 무지개 효과 같은 것을 생성하기 위해서, 그러나 그것은 이 챕터의 범위를 벗어납니다. (더 많은 정보를 얻기 우해서 Rewer 2004를 참고하세요)
16.2.2 The Phase Function
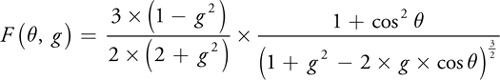
위상함수(The phase function)은 각도(그림16-2의 2개의 초록색 반직선 사이 각도)와 산란의 대칭에 영향을 주는 상수 g값을 기반으로 얼마나 많은 라이트가 카메라방향을 향해서 산란되어지는지 설명합니다. 많은 다른 종류의 위상함수가 있습니다. 이것은 Nishita et al(1993)에서 사용되어진 Henyey-Greenstein 의 적응입니다.
Rayleigh 산란은 g를 0으로 설정하여 근사되어질 수 있습니다, 그리고 그것은 방적식을 크게 단순화 시키고 양의 그리고 음의 각들에 대해서 대칭을 만듭니다. g가 음의 값이면 앞쪽 방향으로 더 산란합니다, 그리고 g가 양의 값이면 광원방향으로 더 많이 산란합니다. Mie의 Aerosol 산란의 경우, g는 보통 -0.75와 -0.999사이 값으로 설정합니다. 방정식을 0으로 만드는 경우가 있을 수 있기 때문에, g가 1이나 -1로는 절대로 설정되지 않습니다.
16.2.3 The Out-Scattering Equation

Out-scattering 방정식은 앞서 언급했던 내부 적분입니다. 적분 부분은 "optical depth"를 결정하거나 점 Pa에서 Pb를 지나는 반직선에서의 평균 대기의 밀도에 광선의 길이를 곱한 것입니다. 이것은 역시 "optical length" 혹은 "optical thickness"라고 불립니다. 얼마나 많은 공기 입자가 반직선을 따라 지나는 빛의 경로에 있는지에 기반한 가중치 요소로 봅니다. 나머지 방정식은 상수로 구성됩니다, 그리고 그들은 라이트에서 얼마나 많은 입자들이 반직선으로 부터 산란되는지 결정합니다.
이 적분값을 계산하기 위해서, Pa로 부터 Pb로 향하는 반직선은 여러부분으로 나눌 것입니다. 그리고 지수항은 각 샘플 포인트에서 평가되어집니다. 변수 h는 샘플 포인트의 높이 입니다. 내 구현에서, 0은 바다를 그리고 1은 대기의 상단부분을 나타내기 위해서, 높이가 Scale되어 집니다. 이론적으로, 대기는 고정된 상단 부분이 없습니다, 그러나 현실적인 목적을 위해서, 우리는 Sky dome을 그릴 특정 높이를 선택해야만 합니다. H0은 대기의 평균 밀도를 발견한 높이인 Scale 높이 입니다. 내 구현은 0.25를 사용합니다, 그래서 평균 밀도는 지상에서 Sky dome으로 가는 25 퍼센트 지점입니다.
상수는 빛의 파장(혹은 컬러)이고 K()는 산란 상수입니다, 그리고 그것은 바다 레벨의 대기밀도에 의존합니다. Rayleigh 와 Mie 산란은 각각 그들의 Scale 높이(H0)을 포함한 산란 상수들이 있습니다, Rayleigh 와 Mie 산란은 파장에 의존되는 방식이 다릅니다. Rayleigh 산란 상수는 보통 4로 나누어집니다. 대부분의 컴퓨터 그래픽스 모델에서, Mie 산란 상수는 파장에 의존하지 않습니다, 그러나 적어도 특정 구현은 그것을 0.84로 나눕니다. 이 방정식이 파장에 의존하던 말던, 3가지 각각의 컬러 채널과 산란의 유형별로 분리해서 문제를 풀어야 합니다.
16.2.4 The In-Scattering Equation
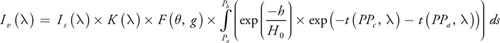
In-scattering 방정식은 태양으로 부터 산란되는 라이트 때문에 얼마나 많은 라이트가 대기를 통과하는 반직선에 추가되어지는지 나타냅니다. Pa에서Pb까지의 반직선 상의 각 점 P에 대해서, PPc는 점에서 태양까지의 반직선이고 PPa는 샘플 포인트에서 카메라로의 반직선입니다. Out-scattering 함수는 그림16-2의 2개의 초록색 반직선을 따라서 얼마나 많은 라이트가 산란되어지는 결정합니다. 남은 라이트는 위상 함수에 의해서, 산란 상수, 그리고 태양광의 강도, Is()에 의해서 조정됩니다. 태양광의 강도는 파장에 종속되지 않아도 되지만 만약 당신이 보라색 별의 주위를 회전하는 외계인 세상을 만들고 싶다면 이곳이 바로 당신이 컬러를 적용할 곳입니다.
16.2.5 The Surface-Scattering Equation

표면으로 부터 반사되어지는 라이트를 산란하기 위해서, 행성 표면과 같은, 당신은 반사되어진 라이트의 일부가 카메라 방향으로 산란되어질 것이라는 사실을 고려야만합니다. 게다가, 추가 라이트는 대기에서 산란되어집니다. le()는 표면에서 방출되거나 반사된 라이트의 양입니다, 그래서 lv()만 하늘을 렌더링하는데 필요합니다.
표면에 의해서 얼마나 많은 라이트가 반사되거나 방출되는지 결정하는 것은 어플리케이션에 따라 다릅니다, 그러나 반사된 태양광에 대해서, 태양광이 표면을 때리기 전에 발생하는 out-scattering을 고려해야합니다(이것입니다, Is () x exp(-t(Pc Pb ,))), 그리고 얼마나 많은 라이트가 표면에 반사되었는지 결정할때 그것을 라이트 컬러로 사용합니다.
16.3 Making It Real-Time
이전 섹션에서 설명한대로 in-scattering 방정식을 위해 5개의 샘플 포인트 그리고 out-scattering 방정식을 계산하기위해서 각각의 적분을 위한 5개의 샘플 포인트로 구현하면 얼마나 성능이 저하되는지 알아봅시다. 이것은 각 정점에 대한 함수를 평가하기 위해서 5 x (5 + 5) 샘플들을 제공합니다. 우리는 또한 2가지 산란 타입을 가집니다, Rayleigh 그리고 Mie, 그리고 우리는 3개의 컬러채널(RGB)의 서로다른 파장에 대해서 계산해야만 합니다. 그래서 이제 대략 2 x 3 x 5 x (5 + 5)정도가 됩니다, 혹은 버택스당 300회 계산으로 생각할 수 있음. 설상가상으로, 각 적분 마다 5개의 샘플만 사용한 경우 시각적 품질이 눈에 띄게 저하됩니다. O'Neil 2004는 50개의 샘플들을 내부 적분(inner integrals) 그리고 외부 적분(outer integrals)를 위해서 5개를 사용했습니다. 그리고 그것은 버택스당 계산 수를 3,000개 까지 증가시킵니다!
이것은 아주 느리게 작동할 것이므로, 더 이상 알아볼 필요는 없습니다. Nishita et al(1993)은 미리 계산되어진 2D 조회 테이블을 계산의 수를 반으로 줄이기 위해서 사용하였습니다, 그러나 여전히 리얼타임에서 작동하지 않을 것입니다. 조회 테이블은 태양이 아주 멀리 떨어져있어서 반직선이 평행일 수 있다는 사실을 이용했습니다. (이 아이디어는 섹션 16.2.4의 in-scattering 방정식에 반영 됩니다). 레이가 태양으로 부터 대기내의 특정 지점으로 이동하는 반직선에 대해서 out-scattering의 양을 포함하는 조회테이블 계산을 가능하게 해줍니다. 이 테이블은 out-scattering 적분 중 하나를 그것의 변수가 태양에 대한 고도와 각도인 조회 테이블로 대체합니다. 카메라로 향하는 반직선은 평행하지 않기 때문에 카메라 반직선에 대한 out-scattering 적분은 여전히 런타임에 풀어야 합니다.
O'Neil 2004에서, 나는 두가지 out-scattering 적분을 피할 수있게 해주는 더 나은 2D 조회 테이블을 제안하였습니다. 첫번째 차원, x,는 행성위의 특정 고도의 샘플 포인트를 가집니다, 여기서 0.0은 지상 그리고 1.0은 대기의 꼭대기입니다. 두번째 차원, y, 는 수직 각도를 나타냅니다, 여기서 0.0은 위쪽 그리고 1.0은 아래쪽입니다. 테이블의 각 (x, y) 쌍에서, 반직선은 특정 고도 x에서의 대기의 상단까지 y를 따라서 발사됩니다. 조회 테이블은 4개의 채널을 가집니다, 2개는 Rayleigh 산란을 위해 예약되었고 2개는 Mie 산란을 위해 예약되었습니다. 한 채널은 간단히 고도에서의 대기의 밀도를 포함합니다, 혹은 exp(-h/H0). 다른 채널은 방금 설명한 반직선의 optical depth를 포함합니다. 조회 테이블은 미리 계산되기 때문에에 우리는 optical depth 적분을 근사하기 위해서 50개의 샘플을 사용하기로 했고, 매우 정확한 결과를 도출하였습니다.
Nishita et al(1993)에서 제안한 조회 테이블 처럼, 우리는 대기안의 특정 샘플 포인트로 부터 태양으로의 반직선에 대한 optical depth를 얻을 수 있습니다. 우리가 필요한 것은 샘플 포인트 (x)의 높이 그리고 태양 (y)로의 수직 각도, 그리고 우리는 (x, y)를 테이블에서 조회합니다. 이것은 out-scattering 계산 중 하나를 제거할 수 있습니다. 게다가 카메라로 향하는 반직선에 대한 optical depth는 같은 방식으로 찾을 수 있습니다, 그렇죠? 좋습니다, 거의 다왔습니다. 카메라가 우주에 있을 때도 동일한 방식으로 동작합니다, 그러나 카메라가 대기안에 있을때는 그렇지 않습니다. 왜냐하면 조회테이블에 사용된 샘플 반직선들은 높이 x에서의 샘플 포인트로 부터 대기의 상단까지 이동하기 때문입니다. 그들은 카메라가 대기 안쪽에 있는 경우가 필요하기 때문에 대기의 중간 쯤 특정 위치에서 멈추지 않습니다.
다행이도, 이것의 해결책은 간단합니다. 첫째로 우리는 카메라를 통과하여 대기의 상단까지 이동하는 반직선의 optical depth를 얻기위해서 샘플 포인트 P로부터 카메라까지 조회합니다. 그리고나서 우리는 같은 반직선에 대해서 2번째 조회를 합니다, 그러나 P에서 시작하는 대신에 카메라에서 시작합니다. 이것은 우리가 원하지 않는 반직선 부분에 대한 optical depth를 줄 것입니다, 그리고 우리는 그것을 첫번째 조회 결과로 부터 뺄 수 있습니다. 이것을 그림으로 표현하는 그림16-3에서 지면의 정점(B1)으로 부터 반직선이 확인하세요.

한가지 문제만 남았습니다. 대기 안의 카메라보다 위쪽에 정점이 있는 경우, 샘플 포인트 P에서 카메라를 통과하는 광선은 행성 자체를 통과할 수 있습니다. 높이 변수는 지금까지는 음수가 될거라 예상되지 않습니다, 그리고 조회 테이블 안의 숫자들은 아주 높은 숫자가 될 수 있어서, 정밀도를 잃고 가끔 부동소수점 오버플로우를 만날 수 있습니다. 이 문제를 피하기 위한 방법은 정점이 카메라 위에 있을 때 반직선의 방향을 반대로 하는 것입니다. 이것을 그림으로 표현하는 그림 16-3에서 반직선이 하늘의 정점(B2)를 지나는 것을 확인해보세요.
이제 우리는 정점당 3,000 번의 계산을 거의 2 x 3 x 5 x (1 + 1), 혹은 60(eye의 반직선을 위한 out-scaterring 적분을 위해서 5번의 샘플을 한다고 가정) , 정도로 줄였습니다,
16.4 Squeezing It into a Shader
이 지점에서, 나는 이 알고리즘이 가능한 만큼 최대한 압축되었다고 느꼈습니다, 그러나 그것을 쉐이더 맞게 하려면 더 작게 압축해야하는 것을 알고있었습니다. 나는 이 알고리즘이 Shader Model 3.0을 요구하길 원하지 않았습니다, 그래서 Vertex Shader 사용되는 텍스쳐에서 조회 테이블은 불가능 했습니다. 나는 다른 접근법을 사용하기로 결정했고 조회 테이블의 결과를 수학적으로 분석하기 시작했습니다. 내가 적분 방정식을 단순화할 방법을 찾을 수 없다는 것을 알았지만, 완전히 다른 방정식으로 충분히 비슷한 결과를 시뮬레이션 할 수 있을지도 모른다고 희망했습니다.
16.4.1 Eliminating One Dimension
나는 조회 테이블의 결과를 그래프에 그리기 시작했습니다. 나는 x축을 따라 0.0에서 1.0까지 높이를 표시했고 조회테이블의 결과 (optical depth)는 y축을 따라 표시했습니다. 0에서 1까지 다양한 샘플링된 각도에 대해서 나는 그래프에 별도의 선을 그렸습니다. 나는 각 선이 x가 0에서 1로 가면서 지수적으로 떨어지는 것을 바로 알아챘습니다, 그러나 그래프에서 각 라인의 scale은 상당히 다양하였습니다. 반직선의 각도가 위쪽 방향에서 아래쪽으로 변하기 때문에 반직선의 길이는 크게 증가하기 때문에 옳바른 결과입니다.
각 선의 곡선의 모양 비교를 쉽게하기 위해서, 그들을 정규화하기로 결정하였습니다. 각 선에 대해서 x=0 에서의 Optical depth 값으로 선에 있는 모든 값들을 나누었습니다. 그래프에서 scale 된 모든 선들은 (x = 0, y = 1)에서 시작하고 (x = 1, y = 0)방향으로 내려갑니다. 놀랍게도, 정규화된 거의 모든 선들은 서로서로 위에 겹쳐졌습니다! 모든 라인의 곡선은 거의 정확히 같았습니다, 그리고 그 곡선은 exp(-4x)였습니다.
이게 말이 되는게, optical depth 방정식은 exp(-h/H0)의 적분입니다. 나는 H0을 0.25가 로 선택하였습니다, 그래서 exp(-4h)는 공용 요소입니다. 그러나 적분안에 있는 h가 적분의 바깥에 있는 높이 x(반직선의 시작에서의 높이)와 같지 않기 때문에 여전히 조금 혼란스럽습니다. 적분안에 있는 h 값은 선형적으로 변하지 않습니다, 그리고 그것은 시작 높이 보다 구형 공간을 통과하는 것과 더 관련있습니다. 선들에는 약간의 변화가 있습니다, 그리고 변화는 각도가 증함에 따라 증가합니다. 각도가 90도보다 더 증가하면 변화가 지수적으로 나빠집니다. 왜냐하면 우리는 90도 보다 더 큰 각도를 다루지 않기 때문입니다(반직선이 행성을 통과해버리기 때문에), exp(-4x)는 조회 테이블의 x축을 제거하는데 효과적입니다.
16.4.2 Eliminating the Other Dimension
이제 조회 테이블의 x 차원 (높이)이 exp(-4x)로 처리되고 있습니다, 우리는 y 차원 (각도)를 제거할 필요가 있습니다. exp(-4x)로 처리 되지 않는 Optical depth의 부분의 유일한 부분은 이전에 설명한 그래프에서 선들을 정규화 할때 사용한 scale 입니다, 그리고 그것은 x = 0 일때의 Optical depth 값입니다. 이제 우리는 x 축에서 0에서 1까지의 각도 그리고 y축은 각 각도의 scale를 새로운 그래프를 만듭니다. 더 나은 이름이 없어서, 나는 이것을 scale 함수라 부릅니다.
내가 처음 scale 함수를 봤을 때, 나는 그것이 0.25(scale 높이)에서 시작한다는 것을 알았고 일종의 가속 곡선을 그리면서 증가했습니다. 그것이 지수적일 수 있다는 생각에, 나는 scale을 scale 높이로 나누었습니다(그래프의 시작이 1에서 이도록 만들기 위해) 그리고 그 결과는 자연로그 였습니다. 그 결과는 내가 알지 못했던 또다른 가속 곡선이었습니다. 나는 여러가지 곡선을 시도해봤지만 곡선의 모든 부분에 잘 맞는 것은 없었습니다. 나는 곡선에 대해 "best fit" 방정식을 찾기 위해서 그래프 분석 소프트웨어를 사용하였습니다, 그리고 그것은 예쁘진 않지만 잘 맞는 값들을 가진 다항식을 얻었습니다.
이 구현의 한가지 큰 단점은 scale 함수가 scale 높이와 대기두께와 행성의 반지름 사이의 비율에 종속된다는 점입니다. 만약 두 값중 하나가 변하면, 당신은 새로운 scale 함수를 계산해야합니다. 이 책의 CD에 포함된 데모에서 대기의 두께(지면에서 대기의 꼭대기의 거리)는 행성 반지름의 2.5 퍼센트 입니다, 그리고 scale 높이는 대기 두께의 25 퍼센트입니다. 이 2개의 값이 동일 값으로 유지된다면 행성의 반지름은 중요하지 않습니다.
16.5 Implementing the Scattering Shaders
이제 수학적으로 문제가 해결되었습니다, 데모가 어떻게 구현되었나 살펴봅시다. 데모를 위한 C++ 코드 꽤 간단합니다. gluSphere() 함수는 지면과 Sky dome을 그리기 위해서 호출됩니다. sky dome은 Sphere가 내부에서 렌더링되므로 앞쪽면이 반대입니다. 지면 산란이 지면의 컬러에 영향을 미치는 것을 볼수있게 하기위해 간단한 사각형의 Earth 텍스쳐를 사용합니다, 그리고 간단한 glow 빌보드 텍스쳐를 사용하여 달을 렌더링 합니다. 뚜렷한 모양의 태양은 렌더링하지 않습니다만 Mie 산란은 Sky dome에서 태양과 같이 생긴 Glow를 만듭니다(오직 대기를 통해서 볼때만).
나는 이책의 CD에 Cg와 GLSL 두가지 구현을 모두 제공했습니다. 지면, 하늘, 우주에서 오브젝트들은 2개의 산란 쉐이더를 가집니다, 하나는 카메라가 우주안에 있을때 그리고 하나는 카메라가 대기안에 있을때 (이것은 쉐이더에서 조건 분기문을 피하게 해줍니다). 지면 쉐이더는 카메라 아래의 오브젝트들 뿐만아니라 지형을 위해서 사용할 수 있습니다. 하늘 쉐이더는 카메라 위에 있는 오브젝트들 뿐만 아니라 Sky dome에 사용될 수 있습니다. 우주 쉐이더는 대기의 바깥에 있는 달과 같은 특정 오브젝트에 사용될 수 있습니다.
쉐이더 네이밍 규약은 "render_object from camera_position" 입니다. 그래서 SkyFromSpace 쉐이더는 카메라가 우주에 있을때 Sky dome을 렌더링 하기 위해서 사용됩니다. 쉐이더에서 전체에서 사용하는 공통 상수와 헬퍼 함수들을 위한 공용 쉐이더도 있습니다. SkyFromSpace를 예제로 사용해봅시다.
16.5.1 The Vertex Shader
리스트 16-1에서 보는것 처럼, SkyFromSpace.vert는 꽤 복잡한 Vertex Shader입니다만 코드에서 주석과 여기서 제공하는 설명으로 따라가기 충분히 쉽습니다. Kr은 Rayleigh 산란 상수입니다, Km은 Mie 산란 상수, 그리고 ESum은 태양의 밝기 입니다. Rayleigh는 다른 라이트 파장을 다른 비율로 산란시킵니다, 그리고 비율은 1/pow(wavelength, 4) 입니다. 그림 16-2를 다시 참조해보면, v3Start는 이전 예제에서 점 A이고 v3Start + fFar * v3Ray는 점 B입니다. v3SamplePoint 변수는 반복문의 각 반복들을 통해 P1에서 Pn으로 이동합니다.
fStartOffset 변수는 점 A에서 카메라로 향하는 조회테이블의 실제 값입니다. 대기의 바깥쪽 가장자리에서 우리는 왜 이것을 계산할 필요가 있을까요? 바깥쪽 가장자리에서의 밀도가 실제로 0이 아니기 때문입니다. 밀도의 지수적으로 감쇄하고 그것의 거의 0이 됩니다, 그러나 만약 우리가 이 값을 계산하지 않고 offset을 사용한다면, 카메라가 대기에 들어가게 될때 컬러가 급격하게 변할 것입니다.
위상함수가 쉐이더에서 빠져있는 것을 알아챘을 건데요. 위상함수는 라이트로 향하는 각도에 의존합니다, 그리고 만약 Vertex 당 계산하게 되면 이것은 테셀레이션 아티팩트로 고통받습니다. 이 아티팩트를 피하기 위해서, 위상함수는 Fragment Shader에서 구현되어집니다.
예제 16-1. SkyFromSpace.vert, Which Renders the Sky Dome When the Camera Is in Space
#include "Common.cg"
vertout main(
float4 gl_Vertex : POSITION,
uniform float4x4 gl_ModelViewProjectionMatrix,
uniform float3 v3CameraPos, // The camera's current position
uniform float3 v3LightDir, // Direction vector to the light source
uniform float3 v3InvWavelength, // 1 / pow(wavelength, 4) for RGB
uniform float fCameraHeight, // The camera's current height
uniform float fCameraHeight2, // fCameraHeight^2
uniform float fOuterRadius, // The outer (atmosphere) radius
uniform float fOuterRadius2, // fOuterRadius^2
uniform float fInnerRadius, // The inner (planetary) radius
uniform float fInnerRadius2, // fInnerRadius^2
uniform float fKrESun, // Kr * ESun
uniform float fKmESun, // Km * ESun
uniform float fKr4PI, // Kr * 4 * PI
uniform float fKm4PI, // Km * 4 * PI
uniform float fScale, // 1 / (fOuterRadius - fInnerRadius)
uniform float fScaleOverScaleDepth) // fScale / fScaleDepth
{
// Get the ray from the camera to the vertex and its length (which
// is the far point of the ray passing through the atmosphere)
float3 v3Pos = gl_Vertex.xyz;
float3 v3Ray = v3Pos - v3CameraPos;
float fFar = length(v3Ray);
v3Ray /= fFar;
// Calculate the closest intersection of the ray with
// the outer atmosphere (point A in Figure 16-3)
float fNear = getNearIntersection(v3CameraPos, v3Ray, fCameraHeight2,
fOuterRadius2);
// Calculate the ray's start and end positions in the atmosphere,
// then calculate its scattering offset
float3 v3Start = v3CameraPos + v3Ray * fNear;
fFar -= fNear;
float fStartAngle = dot(v3Ray, v3Start) / fOuterRadius;
float fStartDepth = exp(-fInvScaleDepth);
float fStartOffset = fStartDepth * scale(fStartAngle); // Initialize the scattering loop variables
float fSampleLength = fFar / fSamples;
float fScaledLength = fSampleLength * fScale;
float3 v3SampleRay = v3Ray * fSampleLength;
float3 v3SamplePoint = v3Start + v3SampleRay * 0.5; // Now loop through the sample points
float3 v3FrontColor = float3(0.0, 0.0, 0.0);
for(int i=0; i<nSamples; i++)
{
float fHeight = length(v3SamplePoint);
float fDepth = exp(fScaleOverScaleDepth * (fInnerRadius - fHeight));
float fLightAngle = dot(v3LightDir, v3SamplePoint) / fHeight;
float fCameraAngle = dot(v3Ray, v3SamplePoint) / fHeight;
float fScatter = (fStartOffset + fDepth * (scale(fLightAngle) - scale(fCameraAngle)));
float3 v3Attenuate = exp(-fScatter * (v3InvWavelength * fKr4PI + fKm4PI));
v3FrontColor += v3Attenuate * (fDepth * fScaledLength);
v3SamplePoint += v3SampleRay;
}
// Finally, scale the Mie and Rayleigh colors
vertout OUT;
OUT.pos = mul(gl_ModelViewProjectionMatrix, gl_Vertex);
OUT.c0.rgb = v3FrontColor * (v3InvWavelength * fKrESun);
OUT.c1.rgb = v3FrontColor * fKmESun;
OUT.t0 = v3CameraPos - v3Pos;
return OUT;
}
16.5.2 The Fragment Shader
이 쉐이더는 꽤 자명합니다. 리스트 16-2에서 보여주지 않은 것은 하나는 getRayleighPhase() 함수안의 수학 부분을 주석처리 한것입니다. Rayleigh 위상 함수는 각도 0와 180도에서 가장 밝고 90도에서 가장 어두운 파란색 하늘을 만듭니다. 그러나, 나는 90도 근처에서 하늘이 너무 어둡다고 느낍니다. 이론적으로, 우리가 여러번의 산란을 구현하지 않았기 때문에 문제가 됩니다. 단일 산란은 태양에서 부터 오는 라이트가 얼마나 많이 산란되는지만 계산합니다. 광선의 경로로에서 산란되어진 라이트는 사라집니다. 여러번의 산란은 라이트가 어디로 갔는지 찾아내려고 합니다, 그리고 종종 다른 각도로 부터 카메라 방향으로 되돌아 옵니다. 이것은 Radiosity 라이팅과 아주 유사합니다, 그리고 이것은 리얼타임에 계산을 고려하지 않습니다. Nishita et al(1993)은 ambient 요소를 어두운 영역을 밝히는데 사용합니다. 나는 Rayleigh 위상 함수를 완전하게 제거하는 것이 더 보기 좋다고 느꼈습니다. 마음껏 가지고 놀아보고 당신이 가장 마음에 드는 것을 찾아보세요.
예제 16-2. SkyFromSpace.frag, Which Renders the Sky Dome When the Camera Is in Space
#include "Common.cg"
float4 main(
float4 c0 : COLOR0,
float4 c1 : COLOR1,
float3 v3Direction : TEXCOORD0,
uniform float3 v3LightDirection,
uniform float g,
uniform float g2) : COLOR
{
float fCos = dot(v3LightDirection, v3Direction) / length(v3Direction);
float fCos2 = fCos * fCos;
float4 color = getRayleighPhase(fCos2) * c0 + getMiePhase(fCos, fCos2, g, g2) * c1;
color.a = color.b;
return color;
}
16.6 Adding High-Dynamic-Range Rendering
대기 산란은 High-dynamic-range(HDR) 렌더링 없이는 좋게 보리지 않습니다. 이 방정식들은 쉽게 아주 밝거나 아주 어두운 이미지를 만들 수 있기 때문입니다. 그림16-4를 보세요. 부동소수점 버퍼에 이미지를 렌더링 하고 컬러를 0..1로 조정 가능한 노출 상수를 사용한 지수 곡선으로 scale 하는 것이 더 좋게 보입니다.

이 대모에서 사용된 노출 방정식은 아주 간단합니다: 1.0 - exp(fExposure x color). 노출 상수는 카메라의 조리개나 당신의 눈에 동공같이 작동합키다. 너무 밝다면, 노출 상수는 라이트가 적게 들어오게 하기 위해 감소됩니다. 라이트가 충분하지 않다면, 노출 상수는 더 많은 라이트가 들어오게 하기위해서 커집니다. 노출상수에 합당한 제한 없이, 대낮이 달빛으로 혹은 반대 경우로 보여질 수 있습니다. 그럼에도 불구하고, 각 컬러의 상대 밝기는 항상 보존됩니다.
이 데모에서 구현된 HDR 렌더링은 아주 간단합니다. 부동소수점 필셀 포맷으로 생성된 OpenGL pbuffer를 상상하고 렌더 투 텍스쳐를 활성화합니다. 이전에 사용한 같은 렌더링 코드를 사용합니다만 모든것은 pbuffer의 렌더링 컨텍스트에 그려집니다. 그후, 메인 렌더링 컨텍스트가 선택되어지고 단일 Quad가 전체 스크린을 채우기 위해 그려집니다. 부동소수점 버퍼는 텍스쳐류 선택되어집니다, 그리고 간단한 지수 scaling shader가 컬러를 0-255 범위 조정 하는데 사용되어 집니다. 노출 상수는 수동으로 설정되고 여러 산란 상수의 사용에 따라 데모에서 런타임에 변경될 수 있습니다.
다행히도, 현대 GPU는 부동소수점 렌더타겟울 지원합니다. 알파 블랜딩 같은 몇몇 중요한 특징은 당신이 GeForce 6 시리즈 GPU를 사용할때까지 사용 불가능합니다, 그래서 Sky dome과 우주에서 그려지는 오브젝트들의 블랜딩 오래된 GPU에서 작동하지 않을 것입니다.
16.7 Conclusion
비록 설명한 모델로 대화식으로 장면을 렌더링할 수 있게 할 수 있으려면 꽤 많은 단순화가 필요했습니다만, 데모는 특히 HDR 렌더링에서 꽤 선명하게 보입니다. 시스템의 파라메터를 조정하는 것은 즐거움의 근원이 될 수 있습니다; 만약 우리의 대기가 약간 다껍다면 나는 지평선에서의 하늘이 정오에 오랜지색이라거나 일몰이 더 멋질 것이라는 것을 상상하지 못했습니다. 빨강과 오랜지색 하늘은 서로다른 파란색 음영의 일몰을 만듭니다, 그리고 보라색 하늘은 초록색 일몰을 만듭니다. 심지어 한번은 무지개 일몰을 생성하는 설정을 찾았었습니다.
어떤 경우든, 작업은 여기서 완료되지 않았습니다. 이 알고리즘을 개선할 수 있는 여러가지 방법이 있습니다:
- 특정 scale 높이와 대기의 두께와 행성의 반경의 비율을 하드코딩 하지 않은 대기-밀도 scale 함수의 생성
- Rayleight 와 Mie 산란이 서로다른 scale depth를 가질 수 있도록 분리
- 여러번의 산란을 시뮬레이션 하기위한 더 나은 방법 제공 그리고 Rayleight 위상함수 다시 사용
- 태양뿐만 아니라 달과 같은 다른 소스의 라이트를 산란 가능케 하기. 이것은 달을 감사는 후광(halo)으로 달빛 효과를 만들기 위해 필요할 것입니다.
- 대기 산란은 또한 거리가 있는 오브젝트들이 실제보다 더 크고 흐리게 보이게 만듭니다. 만약 우리가 대기를 통해서 보지 않는다면 달은 더 우리에게 더 작게 보일 것입니다. 이것은 HDR 패스에서 Optical depth를 기반으로 한 블러링 필터와 같은 것을 통해 얻어질 수 있습니다.
- 반직선을 따라서 얻은 샘플 포인트를 고도에 따라서 선형에서 지수로 변경합니다. Nishta et al(1993)은 이것이 왜 이득이 되는지 설명합니다.
- 구름, 강수, 번개 그리고 무지개 같은 다른 대기 효과를 추가합니다. Harris 2001, Brewer 2004 그리고 Dobashi et al(2001)을 보세요.
16.8 References
Brewer, Clint. 2004. "Rainbows and Fogbows: Adding Natural Phenomena." NVIDIA Corporation. SDK white paper. http://download.nvidia.com/developer/SDK/Individual_Samples/DEMOS/Direct3D9/src/HLSL_RainbowFogbow/docs/RainbowFogbow.pdf
Dobashi, Y., T. Yamamoto, and T. Nishita. 2001. "Efficient Rendering of Lightning Taking into Account Scattering Effects due to Clouds and Atmospheric Particles." http://nis-lab.is.s.u-tokyo.ac.jp/~nis/cdrom/pg/pg01_lightning.pdf
Harris, Mark J., and Anselmo Lastra. 2001. "Real-Time Cloud Rendering." Eurographics 2001 20(3), pp. 76–84. http://www.markmark.net/PDFs/RTClouds_HarrisEG2001.pdf
Hoffman, N., and A. J. Preetham. 2002. "Rendering Outdoor Scattering in Real Time." ATI Corporation. http://www.ati.com/developer/dx9/ATI-LightScattering.pdf
Nishita, T., T. Sirai, K. Tadamura, and E. Nakamae. 1993. "Display of the Earth Taking into Account Atmospheric Scattering." In Proceedings of SIGGRAPH 93, pp. 175–182. http://nis-lab.is.s.u-tokyo.ac.jp/~nis/cdrom/sig93_nis.pdf
O'Neil, Sean. 2004. "Real-Time Atmospheric Scattering." GameDev.net. http://www.gamedev.net/columns/hardcore/atmscattering/
'Graphics > 참고자료' 카테고리의 다른 글
| [번역]Real-Time Atmospheric Scattering (0) | 2020.08.22 |
|---|---|
| [번역] INTRO TO GPU SCALARIZATION – PART 2 -SCALARIZE ALL THE LIGHTS (0) | 2020.08.08 |
| [번역] INTRO TO GPU SCALARIZATION – PART 1 (0) | 2020.07.20 |
| [번역][Nvidia White Paper] Cascaded ShadowMaps (0) | 2020.07.17 |
| [번역]Performance of Array vs. Linked-List on Modern Computers (2) | 2020.07.08 |




