| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- scalar
- RayTracing
- SIMD
- Nanite
- 번역
- Graphics
- Wavefront
- GPU
- DX12
- Study
- forward
- unrealengine
- UE5
- VGPR
- shader
- ShadowMap
- rendering
- SGPR
- scattering
- atmospheric
- optimization
- hzb
- texture
- Shadow
- wave
- DirectX12
- deferred
- vulkan
- GPU Driven Rendering
- ue4
- Today
- Total
RenderLog
[번역+설명추가] Spherical Mapping 본문
개인 공부용으로 번역한 거라 잘못 번역된 내용이 있을 수 있습니다.
또한 원작자의 동의 없이 올려서 언제든 글이 내려갈 수 있습니다.
출처
https://www.opengl.org/archives/resources/code/samples/sig99/advanced99/notes/node176.html
www.opengl.org/archives/resources/code/samples/sig99/advanced99/notes/node177.html
11.2.1 Sphere Mapping

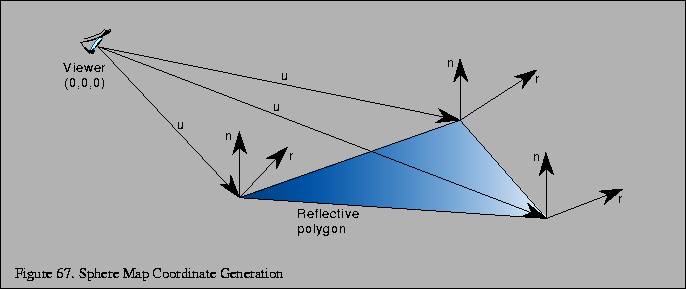
OpenGL은 Sphere 매핑으로 알려진 환경매핑을 매개변수화하여 기본 지원합니다. Sphere 매핑은 Orthographic Projection을 사용하여 관찰할 때, 완벽하게 반사되는 반구에서 보는 것과 같은 irradiance 이미지의 환경매핑 종류입니다 [76]. 이 개념은 그림 66 에 있습니다. Sphere map은 Viewing Plane에서 계산됩니다(역주 : Viewing Plane 쪽으로 반사 벡터를 투영시킴). 평면의 Width와 Height는 Sphere의 지름과 일치합니다. Orthographic projection을 사용하여 발사된 반직선(Ray)들은 파란색(검 회색). Sphere의 중심에서, 반직선은 관찰자에게 다시 반사됩니다. Sphere의 가장자리를 따라서, 반직선은 Sphere와 접하고 Sphere의 뒤로 갑니다.
알아둬야 할 점은 Sphere map은 단일 지점의 irradiance를 계산하기 때문에 Sphere은 무한히 작은 것으로 생각 할 수 있습니다(역주 : Sphere map을 계산할 때, 쓰는 sphere의 크기는 상상할 수 없을 정도로 엄청나게 작은 점이라고 생각하면 됨). 실제로 Sphere의 크기를 0에 근접하도록 제한합니다. 참고로 sphere의 중심으로 발사된 반직선은 관찰자로 바로 반사되어집니다. 또한 Sphere의 silhouetee edge 로 발사된 반직선은 환경에서 구의 뒷면에 있는 지점에 바로 매핑됩니다. (역주 : 그림 66의 노락색 반직선중 맨 아래와 맨 위쪽을 보면 그냥 쭉 지나가는데, 그런식으로 Sphere 의 뒷면에 같은 지점이 매핑된다는 의미)
11.2.1.1 The Mathematics of Sphere Mapping
Eye 위치에서 버택스로의 벡터를 U로 표시하고, 정규화 된 것을 U'로 표현합니다. Eye 좌표계에서 계산되기 때문에 Eye의 위치는 원점에 위치하며 U는 Eye-space에서 버택스의 위치와 일치합니다. 현재 Normal은 은 ModelView 의 Inverse transpose Matrix에 의해 변환되며 정규화 됩니다, 그리고 N'가 됩니다. 반사벡터 R은 아래와 같이 계산될 수 있습니다.

정의:

------------------------------------------------------------------------------
역주 설명 추가, p의 공식 유도 (아래 첨부파일 참고함, 출처 : www.inf.ed.ac.uk/teaching/courses/cg/lectures/slides9.pdf):

여기서 V는 (0, 0, 1)이라고 가정 (Orthogoranl Projection이라 모든 광선이 (0, 0, 1) 가능)
Sphere map에서의 Normal 값(정규화 안됨)은 n = r + v 로 얻을 수 있음.
그렇다면 n = (Rx, Ry, Rz + 1)
정규화한 n은 아래와 같이 구할 수 있음.
n의 크기 : m = root(Rx^2 + Ry^2 + (Rz + 1)^2)
-> 정의: 에 나오는 p는 n의 크기
n의 크기로 나눠주어 정규화 : (Rx/m, Ry/m, (Rz+1)/m) 으로 볼 수 있음.
-> 아래의 공식 8, 9는 정규화된 n의 x, y 값
이 설명으로 Sphere map을 정규화된 Sphere의 Normal Vector의 x, y 컴포넌트로 인뎅싱 하는 것을 알 수 있음.
그리고 (Rx / p) * 1/2 + 1/2 식에서 1/2 곱하고 1/2 더하는 것은 Normal의 값이 [-1, 1] 인데 텍스쳐 좌표는 [0, 1] 범위므로 조정해 주는 것 (아래 설명에 나옴)
실제 구현은 여기 참고 : github.com/scahp/Shadows/tree/SphericalMapping
추가: 360도 방향을 모두 커버해주는 SphereMap은 SphereMap TwoMirrorBall - 360도 방향 커버 됨 이 글 참고
------------------------------------------------------------------------------
그리고나서 텍스쳐 좌표계는 다음과 같이 계산됩니다:
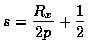

이러한 계산은 OpenGL의 텍스쳐 좌표계 생성 단계에서 내부적으로 계산됩니다. 이 계산은 그림 67과 같이 프리미티브의 각 버택스에 대해서 수행됩니다.
위의 공식은 어렵게 보입니다, 그러나 이 식은 처음 보는 것 같지는 않습니다. 공식7은 주어진 노멀과 입사 벡터에 대한 반사벡터를 구하는 표준 공식입니다. 대부분의 입문 그래픽스 교과서는 간단한 증명과 좋은 설명을 해줍니다.
N'와 U'는 정규화 되었기 때문에, R 또한 정규화 됩니다. R을 단위구(Unit sphere)에서 3D 점이라고 생각할 수 있습니다. 우리가 할일은 3D 점을 2D 좌표계로 만드는 것입니다. 2차원으로 줄이는 것은 R을 Rz = 0인 평면인 단위원위에 투영하여 처리할 수 있습니다. 이게 p로 나눠지는 이유입니다.
R이 정규화되어 있다고 알고있기 때문에, Rx / p 와 Ry / p 는 [-1, 1] 범위에 있어야 합니다. 그러나 2D 텍스쳐으로 인덱싱 하기 위해서, 우리는 [0, 1] 범위가 필요합니다. 공식 8과 9에서, 1/2로 Scale하고 1/2 를 Bias 로 하여(역주 : 1/2를 곱하고 1/2를 더한다는 의미) [-1, 1] 범위를 [0, 1] 범의로 매핑할 수있습니다.
Sphere map을 구성할 때, (s, t)로 부터 R로 매핑하는 것이 필요할 때가 있습니다. 역으로 매핑하는 것은 아래와 같습니다:

Sphere map에서 이미지는 중심이 (1/2, 1/2)이고 원의 반지름이 1/2인 것으로 생각 할 수 있습니다. (1/2, 1/2)를 위의 역 매핑 공식에 연결하면 (0, 0, 1) 반사 벡터를 얻습니다. OpenGL은 Eye가 마이너스 Z 방향 쪽을 내려다 보고 있다고 가정합니다. 그래서 Vector(0, 0, 1)은 Eye에 대해서 바로 반대로 반사되어진 것입니다. 만약 우리가 Sphere map을 크롬볼(Chrome sphere)를 직접 바라보고 있다고 생각하면, 우리 자신이 반사되어 보일 것으로 예상했지만 Sphere의 중심은 보이지 않을 것이라 기대됩니다. (역주 : 정확한 뜻을 모르겠네요 원문은 If we think of a sphere map as what we see when looking directly at a chrome sphere, then dead in the center of the sphere we expect to see our own reflection.)
Sphere map의 원의 가장자리에서 (s, t)좌표계를, 예를들어 (0, 1/2)와 (1/2, 0)를, 역 매핑 공식에 연결시켜 보세요. 원의 가장자리에서의 점에서, 결과는 항상 (0, 0, -1)입니다. 다시말해, 만약 우리가 크롬볼을 볼 때 우리가 Sphere map에서 보는 것을 생각하면, Sphere의 Silhouette edge는 Sphere 바로뒤에 있는 것의 extreme grazing 반사로 보입니다. 만약 이게 말이 안된다면, 사실을 확인하기 위해서 그림 66을 다시보세요. 적절히 생성된 Sphere map에서 Sphere의 가장자리의 모든 점은 동일한 색상이어야 합니다.
마지막으로 Sphere map의 원 바깥의 점에 대한 (s, t) 좌표를 역 매핑 공식에 연결해보세요. (0, 0)과 (1, 1)과 같은 점을 해보세요. Rx 와 Ry에 대한 공식에서 제곱근의 피연산자는 음수가 됩니다. 이것은 놀랍지 않습니다. 왜냐하면 적절히 정규화된 반사 벡터는 Sphere map의 원 내에 들어오도록 생성됩니다.
'Graphics > 참고자료' 카테고리의 다른 글
| [번역] To z-prepass or not to z-prepass – Interplay of Light (0) | 2020.12.24 |
|---|---|
| [번역] Global Illumination Using Progressive Refinement Radiosity (0) | 2020.12.19 |
| [번역]Real-Time Computation of Dynamic Irradiance Environment Maps (0) | 2020.11.26 |
| [번역]WHAT IS SHADER OCCUPANCY AND WHY DO WE CARE ABOUT IT? (0) | 2020.11.13 |
| [번역]A Better Way to Scalarize a Shader (0) | 2020.10.31 |



