| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- DX12
- vulkan
- GPU
- scalar
- Wavefront
- unrealengine
- Nanite
- VGPR
- deferred
- wave
- atmospheric
- rendering
- Shadow
- UE5
- scattering
- Study
- ShadowMap
- Graphics
- 번역
- texture
- DirectX12
- forward
- shader
- optimization
- ue4
- hzb
- SGPR
- GPU Driven Rendering
- RayTracing
- SIMD
- Today
- Total
RenderLog
[번역] Global Illumination Using Progressive Refinement Radiosity 본문
[번역] Global Illumination Using Progressive Refinement Radiosity
scahp 2020. 12. 19. 00:07개인 공부용으로 번역한 거라 잘못 번역된 내용이 있을 수 있습니다.
또한 원작자의 동의 없이 올려서 언제든 글이 내려갈 수 있습니다.
출처 : https://developer.nvidia.com/gpugems/gpugems2/part-v-image-oriented-computing/chapter-39-global-illumination-using-progressive
추가 (2020년 12월 28일)
단어 의미 정리
Form-Factor(폼팩터) : 현재 오브젝트로 부터 다른 오브젝트로 전송되어진 에너지의 비율 (출처 : en.wikipedia.org/wiki/Form_factor)
추가 (2021년 1월 9일)
그림 39-4 빠진 것 추가
Chapter 39. Global Illumination Using Progressive Refinement Radiosity
Greg CoombeUniversity of North Carolina at Chapel Hill
Mark HarrisNVIDIA Corporation
강력한 그래픽스 하드웨어의 등장과 함께, 사람들은 로컬 일루미네이션 모델을 넘어 레이 트레이싱과 라디오시티로 만들 수 있는 더 복잡한 글로벌 일루미네이션 모델을 찾기 시작했습니다. 쉐도우 그리고 Interreflections와 같은 오브젝트간 효과를 통합하는 글로벌 일루미네이션은 로컬 일루미네이션에서 할 수 없는 설득력 있는 수준의 시각적 리얼리즘을 달성합니다.
이 챕터에서, 우리는 모든 계산이 GPU에서 수행되는 라디오시티를 계산하는 방법을 설명합니다. 라디오시티 에너지는 텍셀에 저장됩니다, 그리고 프래그먼트 프로그램은 폼 팩터와 오브젝트간의 가시성을 계산하는데 사용되어집니다. Progressive refinement radiosity의 “gather” 연산을 통해서 우리는 메모리에 있는 임의의 위치에 기록하는 문제를 피합니다. “gather” 연산은 현재 GPU에서 실행할 수 있는 일반적인 메모리 접근 패턴입니다.
그림 39-1은 우리의 시스템에서 글로벌 일루미네이션을 통해 얻을 수 있는 소프트 쉐도우와 간접광(Indirect lighting) 같은 매력적인 효과를 보여준 렌더링 된 이미지 입니다.

39.1 Radiosity Foundations
라디오시티는 글로벌 일루미네이션 문제에 대한 유한-요소(finite-element) 접근입니다(Cohen and Wallace 1993). 장면을 많은 작은 요소들로 나누고 얼마나 많은 에너지가 요소들 사이에 전송되어지는지 계산합니다. 각각의 요소들 사이에 전송된 에너지의 비율은 폼팩터라 불리는 방정식에 의해 설명됩니다. 여기 간단한 버젼의 폼팩터 방정식이 있습니다(Cohen and Wallace 1993), 장면에서의 표면위에 두개의 미소영역 사이의 폼팩터를 제공합니다:

이 방정식은 2개의 부분으로 구성됩니다: 가시성 텀과 지오메트릭 텀입니다. 지오메트릭 텀의 요소 i 와 j 사이에 전송되어진 에너지의 비율이 요소의 거리와 상대적인 방향에 대한 함수임을 나타냅니다. 가시성 텀 V(i, j)는 가려진 요소에 대해서 0이고 완전히 서로가 보이는 텀에서 1입니다.
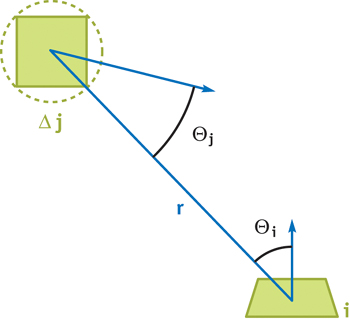
이 공식은 i와 j가 미소한 영역인 경우(혹은 그렇게 다뤄지기 충분히 먼 경우)만 정확합니다. 그러나, 계산의 속도를 증가시키기 위해서, 우리는 넓은 영역의 요소를 사용하기 원하고 이것은 가정을 깨버립니다. 넓은 영역의 요소를 다루는 한 방법은 명시적으로 요소의 영역을 적분하는 것입니다. 이것이 계산상 비싸기 때문에, 우리는 이런 큰 요소를 Oriented-discs를 사용하여 근사합니다(Wallace et al. 1989). 이 접근은 그림 39-2에 있습니다. 그리고 이 상황의 폼팩터는 아래와 같습니다:

39.1.1 Progressive Refinement
고전 라디오시티 알고리즘 (Goral et al. 1984)의 두쌍의 폼팩터로 구성된 대규모 선형 방정식 시스템을 구성하고 해결합니다. 이런 방정식은 그들의 폼팩터와 요소의 반사율 r에 의해 가중치가 부여된 모든 다른 요소로 부터의 에너지 함수로써 요소의 라디오시티를 설명합니다. 그래서 전통적인 선형 시스템은 O(N^2) 저장공간을 요구합니다. 이것은 큰 장면에는 적합하지 않습니다. Progressive refinement 알고리즘(Cohen et al. 1988)은 이러한 폼팩터를 런타임에 계산합니다. 장면의 한 요소에서 다른 모든 요소들로 반복해서 에너지 “shooting”합니다.
여기에 어떻게 progressive refinement가 작동하는지가 있습니다(그림 39-3 알고리즘 2번 반복을 나타냅니다). 장면의 각요소는 두 에너지 값을 유지합니다: 누적된 에너지 값과 잔여(residual)(or “unshot”) 에너지. 우리는 장면에서 요소중 하나를 “shooter”로서 선택하고 이 슈터로 부터 모든 다른 요소의 가시성을 테스트합니다. 만약 받는 요소가 보인다면, 폼팩터와 슈터의 잔여 에너지로 설명된 것 처럼, 우리는 슈터로 부터 전송 받는 요소 방향으로 전송된 에너지의 양을 계산합니다. 다시 반사되어 되돌아오는 에너지의 일부인 이 에너지는 수신자의 반사율이 곱해집니다, 그리고 그것은 보통 RGB 컬러로 표현됩니다. 최종 값은 에너지를 받는 요소의 누적과 잔여 값에 더해집니다. 이제 슈터는 그것의 모든 에너지를 쏩니다, 잔여 에너지는 0으로 설정되고 다음 슈터가 선택되어집니다. 이 과정은 모든 요소의 잔여 에너지가 임계값 값이 이하로 떨어질 때 까지 반복합니다.

처음에, 각 라이트 소스 요소의 잔여에너지는 특정 값으로 설정되고 다른 모든 에너지는 0으로 설정됩니다. 첫번째 반복 이후, 가장 큰 잔여 Power(power = energy x area)를 받은 장면의 폴리곤은 다음번 슈터가 됩니다. 가장 큰 잔여 Power를 선택하는 것은 솔루션이 빠르게 수렴하도록 합니다 (Cohen et al. 1988)
39.2 GPU Implementation
GPU에서 이 알고리즘을 구현하기 위해서, 우리는 텍셀을 라디오시티 요소로 사용합니다(Heckbert 1990). 장면 폴리곤 당 두개의 텍스쳐가 있습니다: 라디오시티 텍스쳐와 잔여 텍스쳐. 텍스쳐를 라디오시티 요소로 사용하는 것은 장면을 균일하게 나누는 것과 비슷합니다. 여기서 텍스쳐의 해상도는 라디오시티 솔루션의 분할 정도를 결정합니다.
만약 Progressive refinement radiosity를 구현하려고 한다면, Shooter의 관점에서 장면을렌더링하는 것을 먼저 시도해야 할 것입니다, 그리고 나서 모든 볼수 있는 폴리곤의 텍스쳐로 에너지를 "splatting" 합니다. 이것이 우리의 첫 접근법이었습니다, 그리고 성능이 좋지 않았습니다. 이 접근법의 문제는 GPU가 여러 텍스쳐들 중 임의의 위치에 기록 한다는 것입니다. 이런 "scatter" 연산 종류는 현재 그래픽 하드웨어에서 구현하기 힘듭니다.
대신, 우리는 수신하는 폴리곤의 반복과 각 요소의 가시성을 테스트 하여 계산을 뒤집습니다. 이것은 많은 텍셀에 대해 동일한 작은 커널 프로그램을 실행하므로써 GPU의 데이터 병렬 특성을 이용합니다. 이 접근은 발사한 라디오시티의 빠른 수렴과 적은 저장공간과 함께 모아진 라디오시티의 고품질로 복원하는 것을 결합합니다. 각 라디오시티 솔루션의 "shot"는 2 패스입니다: 가시성 패스와 재구성 패스입니다. 가시성 패스는 슈터의 입장에서 장면을 렌더링하고 아이템 버퍼에 장면을 저장합니다. 재구성 패스는 모든 수신 폴리곤이 될 가능성 있는 것들을 텍스쳐와 같은 해상도의 프레임버퍼에 직교(Orthographically) 방식으로 렌더링합니다. 이것은 라디오시티의 텍셀과 프레임버퍼의 프래그먼트가 1-1 대응 되도록 합니다. 프래그먼트 프로그램은 가시성을 테스트하고 분석적인(analytic) 폼팩터를 계산합니다. 우리 알고리즘의 수도코드는 리스트 39-1에 나옵니다. 다음 두 섹션은 가시성과 폼팩터 계산에 대해서 더 자세히 설명합니다.
Example 39-1. Pseudocode for Our Algorithm
initialize shooter residual E
while not converged
{
render scene from POV of shooter
for each receiving element
{
if element is visible
{
compute form factor FF
E = * FF * E
add E to residual texture
add E to radiosity texture
}
}
shooter's residual E = 0
compute next shooter
}39.2.1 Visibility Using Hemispherical Projection
폼팩터 방정식의 가시성 텀은 그림 39-4에 나오는 것 처럼 보통 hemicube를 사용하여 계산되어집니다(Cohen and Greenberg 1985). 장면은 cube map의 5면 위에 렌더링됩니다. 그리고 이것이 가시성 테스트에 사용되어집니다. 대신, 우리는 버택스를 hemisphere위에 프로젝션하는 버택스 프로그램을 사용하여 장면을 5번 그리는 것을 피할 수 있습니다. Hemispherical projection은, 또한 Stereographic projection로 알려짐, 한번의 렌더링 패스로 가시성을 계산할 수 있도록 해줍니다. 이기술을 위한 Cg 코드는, 이것은 Prabolic projection(Heidrich and Seidel 1998)과 유사합니다, 리스트 39-2에 나옵니다. 알아둘 점은 z 값은 (x, y) 위치로 부터 분리되어 저장됩니다. 그리고 그것은 옳바른 depth ordering과 관리와 정밀도 이슈를 피하게 합니다.

Example 39-2. Cg Code for Hemispherical Projection
void hemiwarp(float4 Position: POSITION, // pos in world space
uniform half4x4 ModelView, // modelview matrix
uniform half2 NearFar, // near and far planes
out float4 ProjPos: POSITION) // projected position
{
// transform the geometry to camera space
half4 mpos = mul(ModelView, Position);
// project to a point on a unit hemisphere
half3 hemi_pt = normalize( mpos.xyz );
// Compute (f-n), but let the hardware divide z by this
// in the w component (so premultiply x and y)
half f_minus_n = NearFar.y - NearFar.x;
ProjPos.xy = hemi_pt.xy * f_minus_n;
// compute depth proj. independently, using OpenGL orthographic
ProjPos.z = (-2.0 * mpos.z - NearFar.y - NearFar.x); ProjPos.w = f_minus_n;
}Hemispherical projection 버택스 프로그램은 투영된 요소의 위치를 계산합니다, 그리고 프로그래먼트 프로그램은 각 요소의 유니크 ID를 컬러로 렌더링합니다. 이후에, 가시성을 결정할 필요가 있을때, 우리는 프래그먼트 프로그램을 수신자의 ID와 아이템 버퍼의 투영된 위치에서의 ID를 비교하는데 사용합니다. Cg 코드로 된 이 룩업은 리스트 39-3에 나옵니다.
Example 39-3. Cg Code for the Visibility Test
bool Visible(half3 ProjPos, // camera-space pos of element
uniform fixed3 RecvID, // ID of receiver, for item buffer
sampler2D HemiItemBuffer )
{
// Project the texel element onto the hemisphere
half3 proj = normalize(ProjPos);
// Vector is in [-1,1], scale to [0..1] for texture lookup
proj.xy = proj.xy * 0.5 + 0.5;
// Look up projected point in hemisphere item buffer
fixed3 xtex = tex2D(HemiItemBuffer, proj.xy);
// Compare the value in item buffer to the ID of the fragment
return all(xtex == RecvID);
}이 프로세스는 Depth 대신에 폴리곤 ID를 사용하는 것을 제외하면 쉐도우매핑과 아주 비슷합니다. ID를 사용하는 것은 depth 정밀도 문제를 피합니다, 그러나 이것은 빌트인 하드웨어 쉐도우매핑의 이점을 잃습니다(percentage-closer filtering 과 같은)
Hemispherical 프로젝션의 한가지 단점은 폴리곤 에지가 Hemisphere의 커브에 프로젝션 되더라도, 레스터라제이션은 직선 에지를 생성합니다. 이것은 그림 39-5에서 보여줍니다. 이 제한점을 다루기 위해서, 장면 폴리곤은 더 높은 분할 레벨로 테셀레이션 되어져야만 합니다. 그래서 그들이 더 커브 에지에 가깝게 근사되게 할 수 있습니다.

39.2.2 Form Factor Computation
가시성이 결정되면, 우리는 슈터-수신자 폼팩터를 사용하여 슈터로 부터 수신자에게 전송되는 에너지를 계산합니다. 이런 폼팩터 계산은 보통 라디오시티 계산에서 가장 시간을 많이 소비합니다. 우리는 프래그먼트 프로세서의 계산 능력을 활용하기 위해서 프래그먼트 프로그램에서 이것을 구현했습니다.
리스트 39-4는 Cg에서 구현된 폼팩터 계산을 위한 코드를 보여줍니다.
Example 39-4. Cg Code for Form Factor Computation
half3 FormFactorEnergy(
half3 RecvPos, // world-space position of this element
uniform half3 ShootPos, // world-space position of shooter
half3 RecvNormal, // world-space normal of this element
uniform half3 ShootNormal, // world-space normal of shooter
uniform half3 ShootEnergy, // energy from shooter residual texture
uniform half ShootDArea, // the delta area of the shooter
uniform fixed3 RecvColor ) // the reflectivity of this element
{
// a normalized vector from shooter to receiver
half3 r = ShootPos - RecvPos;
half distance2 = dot(r, r);
r = normalize(r);
// the angles of the receiver and the shooter from r
half cosi = dot(RecvNormal, r);
half cosj = -dot(ShootNormal, r);
// compute the disc approximation form factor
const half pi = 3.1415926535;
half Fij = max(cosi * cosj, 0) / (pi * distance2 + ShootDArea);
Fij *= Visible();
// returns visibility as 0 or 1
// Modulate shooter's energy by the receiver's reflectivity
// and the area of the shooter.
half3 delta = ShooterEnergy * RecvColor * ShootDArea * Fij;
return delta;
}39.2.3 Choosing the Next Shooter
Progressive refinement 기술은 가장 높은 잔여 power로 이뤄진 장면 요소로부터 발사되어 빠른 수렴을 이뤄냅니다. 다음 슈터를 찾기위해서, 우리는 간단히 z-buffer 정렬을 사용합니다. mipmap 피라미드는 각각의 요소의 잔여 텍스쳐로 부터 생성됩니다. 이 mipmap 피라미드의 가장 높은 수준, 이것은 전체 텍스쳐의 평균 에너지를 나타냅니다, 텍스쳐에서의 에너지합을 얻기 위해서 텍스쳐 해상도에 곱해집니다. 이런 종류의 감소는 Buck and Purcell 2004와 이 책의 챕터 31 "Mapping Computational Concepts to GPUs"에서 더 깊게 설명합니다.
이 스칼라 값에 폴리곤의 면적이 곱해집니다, 이것은 우리에게 폴리곤의 총 power를 줍니다. 그리고나서 화면 정렬된 사각형(screen-aligned quadrilateral)을 1x1 프레임버퍼에 power의 역수를 depth로 유니크 ID를 컬러로 그립니다. 각 잔여 텍스쳐는 이런 방법으로 그려집니다, 그리고 z-buffering는 자동적으로 가장 높은 power를 가진 폴리곤을 선택합니다. 우리는 다음 슈터의 ID를 얻기 위해서 1 픽셀 프레임 버퍼를 다시 읽습니다. 또한 이 기술은 far clipping plane을 수렴 임계값의 역수로 설정하므로써 우리가 수렴을 테스트하도록 해줍니다. 만약 기록된 프래그먼트가 없다면, 솔루션은 수렴한 것입니다.
39.3 Adaptive Subdivision
이 지점까지, 우리는 라디오시티 텍스쳐가 장면 지오메트리와 1-1 매핑이 되어있다고 가정해왔습니다. 장면이 균일하고 정적으로 테셀레이션되었다는 것을 의미입니다(텍스쳐 해상도에 따라). 그러나 균일한 테셀레이션은 다양한 라이팅의 가변 공간 주파수(variable spatial frequency)에 적용할 수 없습니다. 우리는 쉐도우의 경계 같은 high-frequency 라이팅 영역에서 더 많은 요소를 가지길 원합니다, 그리고 평평한 벽같은 low-frequency 영역에서 더 적은 요소를 원합니다.
39.3.1 Texture Quadtree
이런 문제를 다루는 일반적인 기술은 adaptive meshing solution(Heckbert 1990) 을 사용하는 것입니다. 이 기술을 사용하여, 우리는 장면의 지오메트리를 더 높은 라이팅 변화를 받은 영역을 더 많은 수의 요소로 adaptively 하게 나눠지는 것을 볼 수 있습니다. 우리의 시스템에서, 각각의 장면 폴리곤은 quadtree의 root 처럼 행동합니다, 그리고 라디오 시티 데이터는 tree의 leaf node의 작은(16x16) 텍스쳐에 저장됩니다. 이 계층은 coarse adaptive geometric subdivision 에서 fine uniform texture subdivision으로 생각할 수 있습니다. 그림 39-6 은 장면의 폴리곤이 라이트의 변화에 따라서 더 작은 Quads로 나눠질 수 있다는 것을 보여줍니다.

이러한 접근법을 사용하여, 우리는 균일한 경우에 대해 우리가 개발한 코드를 아주 많이 재사용 할 수 있습니다. 가시성과 슈팅은 각 leaf node에서 계산됩니다(각 장면 폴리곤 대신), 그리고 라디오시티는 비슷한 방식으로 재구성됩니다. 다른점은 우리가 라디오시티를 계산할 때, 우리는 quadtree가 나누어질 것인가를 결정해야만 하는 것 뿐입니다.
39.3.2 Quadtree Subdivision
모든 재구성 패스를 후에, leaf 텍스쳐는 프래그먼트 프로그램을 사용하여 분할을 위해 평가됩니다. 여러 다른 기술이 quadtree 노드가 나눠지는 것을 결정하기 위해서 사용됩니다. 우리는 라디오시티 변화도(Gradient)가 특정 임계값을 넘어가는 경우 노드를 나누는 기술을 사용합니다(Vedel and Puech 1991). 값 대신 변화도를 사용하면 선형 보간으로 그 함수를 적절하게 표현하는 영역에서의 과도한 세분화를 피합니다.
라디오시티의 변화도는 프래그먼트 프로그램에서 평가됩니다, 그리고 변화도의 비연속성이 있는 프래그먼트는 폐기됩니다. 하드웨어 오클루젼 쿼리는 이렇게 폐기된 프래그먼트의 수를 세는데 사용합니다. 만약 폐기된 프래그먼트의 수가 우리의 임계값을 초과하면, 현재 노드는 분할됩니다, 그리고 이 프로세스가 재귀적으로 반복됩니다. 라디오시티가 부드럽거나 최대 깊에 도달한 경우 재귀는 종료됩니다.
39.4 Performance
작은 모델에서 상호작용가능한 수준을 얻기 위해 여러가지 최적화 기술이 있습니다. 우리는 보이지 않은 표면에서의 라디오시티 재구성을 피하기 위해서 오클루젼 쿼리를 가시성 패스에서 사용합니다. 우리는 텍스쳐 해상도보다 낮은 해상도에서 촬영합니다, 이것을 substructing (Cohen et al. 1986) 이라 부릅니다. 이것은 다음 슈터 선택을 위해 생성된 mimaps을 사용하여 처리할 수 있습니다.
만약 다음 슈터인 폴리곤이 선택되었다면, 모든 폴리곤의 요소는 그들의 라디오시티를 차례로 발사합니다. 이것은 여러 shot의 mipmapping 과 정렬 비용을 분할하여 지불합니다. 또한 우리는 컨텍스트 스위칭을 줄이기 위해서 여러 슈터들을 한번에 처리합니다.
이 기술을 사용하여, 우리는 10,000 요소 버젼 코넬박스 장면의 라디오시티 계산을 초당 2프레임 정도에 90% 수렴시킬 수 있었습니다.
리얼타임 어플리케이션에서, 이 기술은 고성능을 위한 표준 렌더링 테크닉과 조합될 수 있습니다. 우리는 라이팅을 간접광이 low frequency라고 가정하여 간접과 직접 일루미네이션으로 분리할 수 있습니다. 이것은 텍스쳐 해상도를 아주 크게 줄여주어, 계산 속도를 증가시킵니다. 라디오시티는 저해상도 텍스쳐를 사용하여 계산합니다, 그리고 직접 일루미네이션은 첫번째 반복 이후 누적된 라디오시티를 0으로 설정하여 지워줍니다. 직접 일루미네이션은 픽셀당 라이팅과 쉐도우볼륨 같은 라이팅 기술을 사용하여 분리되어 계산됩니다. 간접 일루미네이션은 최종 결과 이미지를 얻기 위해서 직접 일루미네이션에 추가됩니다.
39.5 Conclusion
우리는 Progressive refinement radiosity를 사용하여 그래픽스 하드웨어에서 글로벌 일루미네이션을 구현하는 방법을 제안했습니다. 폼팩터 계산을 위해서 프래그먼트 프로세서와 레스터라이제이션 하드웨어의 계산 능력을 사용하여서, 우리는 작은 수의 요소(대략 10,000)의 장면을 상호작용 가능 수준으로 얻을 수 있습니다. 많은 요소의 수를 가진 장면은, 그림 39-7과 같은, 상호작용 불가능한 수준으로 렌더링됩니다. 그래픽스 하드웨어는 계산 속도가 계속해서 증가하고 있기 때문에, 우리는 글로벌 일루미네이션이 라이팅 계산의 일반적인 부분이 될거라 봅니다.

우리는 Hemispherical 프로젝션과 z-buffer 정렬을 포함하고 있는 이 알고리즘을 가속하기 위해서 여러 GPU 트릭을 사용하였습니다. 이러한 것들은 우리가 구현한 것을 넘어 환경 매핑이나 Penetration-depth estimation 같은 더 흥미로은 어플리케이션이 될 수 있습니다.
라디오시티의 한계 중 하나는 diffuse 표면만 표현한다는 것입니다. 이 접근을 diffuse가 아닌 표면으로 확장은 흥미로울 것입니다. 한가지 접근법은 임의의 BRDF를 가진 입사광을 컨볼루션하고 Low-coefficient 다항식 이나 Spherical harmonics(Sillion et al. 1991) 로 결과를 근사는 것입니다.
39.6 References
Buck, I., and T. Purcell. 2004. "A Toolkit for Computation on GPUs." In GPU Gems, edited by Randima Fernando, pp. 621–636. Addison-Wesley.
Cohen, M., S. E. Chen, J. R. Wallace, and D. P. Greenberg. 1988. "A Progressive Refinement Approach to Fast Radiosity Image Generation." In Computer Graphics (Proceedings of SIGGRAPH 88) 22(4), pp. 75–84.
Cohen, M., and D. P. Greenberg. 1985. "The Hemi-Cube: A Radiosity Solution for Complex Environments." In Computer Graphics (Proceedings of SIGGRAPH 85) 19(3), pp. 31–40.
Cohen, M., D. P. Greenberg, D. S. Immel, and P. J. Brock. 1986. "An Efficient Radiosity Approach for Realistic Image Synthesis." IEEE Computer Graphics and Applications 6(3), pp. 26–35.
Cohen, M., and J. Wallace. 1993. Radiosity and Realistic Image Synthesis. Morgan Kaufmann.
Goral, C. M., K. E. Torrance, D. P. Greenberg, and B. Battaile. 1984. "Modelling the Interaction of Light Between Diffuse Surfaces." In Computer Graphics (Proceedings of SIGGRAPH 84) 18(3), pp. 213–222.
Heckbert, P. 1990. "Adaptive Radiosity Textures for Bidirectional Ray Tracing." In Computer Graphics (Proceedings of SIGGRAPH 90) 24(4), pp. 145–154.
Heidrich, W., and H.-P. Seidel. 1998. "View-Independent Environment Maps." In Eurographics Workshop on Graphics Hardware 1998, pp. 39–45.
Sillion, F. X., J. R. Arvo, S. H. Westin, and D. P. Greenberg. 1991. "A Global Illumination Solution for General Reflectance Distributions." In Computer Graphics (Proceedings of SIGGRAPH 91) 25(4), pp. 187–196.
Vedel, C., and C. Puech. 1991. "A Testbed for Adaptive Subdivision in Progressive Radiosity." In Second Eurographics Workshop on Rendering.
Wallace, J. R., K. A. Elmquist, and E. A. Haines. 1989. "A Ray Tracing Algorithm for Progressive Radiosity." In Computer Graphics (Proceedings of SIGGRAPH 89) 23(4), pp. 315–324.
'Graphics > 참고자료' 카테고리의 다른 글
| [번역] Lecture 13: Radiosity - Principles (0) | 2020.12.30 |
|---|---|
| [번역] To z-prepass or not to z-prepass – Interplay of Light (0) | 2020.12.24 |
| [번역+설명추가] Spherical Mapping (0) | 2020.11.29 |
| [번역]Real-Time Computation of Dynamic Irradiance Environment Maps (0) | 2020.11.26 |
| [번역]WHAT IS SHADER OCCUPANCY AND WHY DO WE CARE ABOUT IT? (0) | 2020.11.13 |



