| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- Nanite
- GPU Driven Rendering
- rendering
- shader
- scattering
- wave
- forward
- GPU
- ue4
- SIMD
- scalar
- optimization
- texture
- UE5
- atmospheric
- VGPR
- RayTracing
- deferred
- Study
- ShadowMap
- 번역
- Wavefront
- SGPR
- vulkan
- Graphics
- DirectX12
- hzb
- Shadow
- unrealengine
- DX12
- Today
- Total
RenderLog
[번역] Lecture 13: Radiosity - Principles 본문
개인 공부용으로 번역한 거라 잘못 번역된 내용이 있을 수 있습니다.
또한 원작자의 동의 없이 올려서 언제든 글이 내려갈 수 있습니다.
출처 : https://www.doc.ic.ac.uk/~dfg/graphics/graphics2010/GraphicsLecture13.pdf
Lecture 13: Radiosity - Principles
Reflectance
코스의 초반에 우리는 표면으로부터 반사되는 라이트를 모델링하는 반사율 방정식을 소개했습니다:
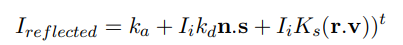
또는 더 간단하게 쓰기 위해 (주어진 ViewPoint에서)

여기서 R은 ViewPoint 에 의존한 반사율 함수입니다.
Radiosity
우리 모델의 주어진 표면(폴리곤)에서 우리는 Radiosity 항을 표면을 떠나는 단위 면적당 에너지로 정의할 수 있습니다. 그것은 폴리곤 표면 전체로 상수가 아닐 것입니다. 그것은 방출된 에너지와 (만약에 있다면) 반사된 에너지의 합니다. 표면의 작은 영역 dA는(이곳에서 방출된 에너지는 상수로 취급할 수 있습니다) 아래와 같습니다:

우리는 이제 장면의 폴리곤을 분산된(distributed) 광원으로 취급합니다. 특정 패치(Patch)로 입사한 에너지는 모든 다른 패치들로 부터 모아집니다, 패치 i는:
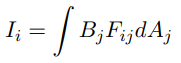
여기서 적분은 i를 제외한 모든 패치를 사용합니다, 그리고 Fij는 패치 i와 패치 j를 연결하는 상수이며 폼팩터(form factor)로 불립니다. 컴퓨터 그래픽스에서 우리는 Continuous solution을 할 수 없습니다, 그래서 우리는 모든 폴리곤을 패치로 나누고 적분의 합으로 교체합니다:

여기서 합은 i를 제외한 모든 패치를 사용합니다 (혹은 Fii=0으로 설정하고 모든 패치들의 합으로 해도 됩니다). 만약 우리가 모든 Bi에 대해서 이 문제를 풀 수 있다면, 올바른 라이트 모델로 각 패치를 직접 렌더링 할 수 있습니다. 식에서 B 값은 패치를 렌더링 하는 데 사용하는 실제 색상입니다, 그래서 B, E 그리고 R 모두는 RGB 컬러 이미지에 대한 3차원 벡터의 양입니다. 폼팩터는 각 RGB 차원에 대해 동일합니다. 우리는 아래의 매트릭스 방정식으로 문제를 공식화할 수 있습니다.
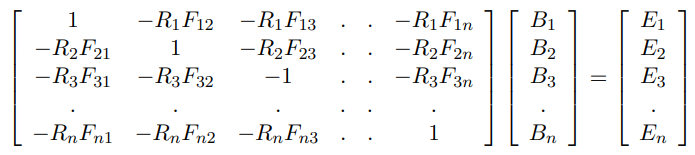
여기서 n은 장면에서의 패치의 수입니다. 폼팩터를 모르기 때문에 답을 구하는게 쉽지 않습니다. 게다가 보통 매트릭스가 50,000 x 50,000 될 것입니다.
우리가 폼팩터의 계산을 고려할때, Specular 반사율이 문제를 유발할 것으로 보입니다. 균일한 Diffuse 반사율과는 다른 점이 어려운 점입니다, Specular 반사율은 방향과 굉장히 의존적이고 광원으로의 방향벡터 v를 포함합니다. 그러나 우리가 언급했듯이, 이제 모든 패치는 광원입니다! 반사광(specularities)에도 문제가 있을 것입니다, 왜냐하면 모든 광원이 더 이상 점(Point)이 아니기 때문입니다, 그래서 우리는 입사광을 Specular cone 모양으로 적분하여야 합니다. 이 모든 것이 반사광(specularities)을 계산하는 것이 매우 어렵다는 것을 의미하므로, 지금은 Diffuse Radiosity만 고려할 것입니다.
이전에 언급한 것 처럼, 우리의 그래픽스 장면을 Radiosity 계산을 위해서 패치로 나눌 필요가 있습니다. 만약 우리의 그래픽스 장면이 작은 폴리곤들로 구성되어있다면, 우리는 폴리곤 맵(polygon map)을 Radiosity 패치 집합으로 사용할 수 있을 것입니다, 그러나 큰 폴리곤의 경우, 벽과 같은, 우리는 이것을 충분히 작게 나누어야 합니다. 왜냐하면 방출하는 라이트가 큰 폴리곤의 모든 부분에서 상수가 아닐 것이기 때문입니다, 그래서 만약 패치가 너무 크다면 우리는 그것을 폴리곤의 분할로 볼 것입니다. 일반적인 환경에서 큰 폴리곤은 음영(shading)의 차이가 있을 것입니다, 또는 폴리곤을 위에 그림자가 드리울 것입니다. 우리는 패치당 한 개의 Radiosity를 계산하기 때문에, 패치의 형태가 원치 않는 atifact로 보일 수 있습니다. 이것을 회피하는 방법은 2가지입니다: (i) 패치 크기를 충분히 작게 하여 (픽셀보다 더 작게) 픽셀 크기로 만듭니다, 또는 (ii) 결과를 부드럽게 만듭니다(즉, Gouraud shading과 유사하게 보간)
The Form Factors
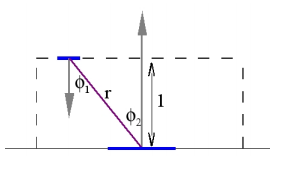
폼팩터는 모든 패치 쌍을 연결하고, 한쪽에서 다른 한쪽에 도달하는 방사에너지(radiated energy)의 비율을 결정합니다. 패치 쌍의 연결은 그림1에 있습니다, 그리고 아래의 방정식을 이용합니다.

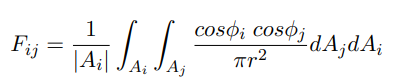
여기서 |Ai|는 패치 Ai의 면적입니다. 두 cos 텀은 두 패치를 연결하는 선에 수직인 방향으로 두 패치의 투영 하도록 합니다. (만약 그들이 직각이면, 빛이 한쪽에서 다른 쪽으로 전달되지 않을 것입니다). 만약 그들이 서로 바라본다면 최대로 연결됩니다(역주: 연결된 선과 패치들의 normal이 일치하면 cos항이 모두 1이 되어 최대 값이 됨). 1/r^2 은 일반적인 빛 강도의 거리에 대한 감쇄를 나타내는 inverse square law입니다. Ai가 충분히 작다고 한다면, 이 방정식을 단순화시킬 수 있습니다. 만약 r이 크다면, Ai의 면적과 비교해서, cos 항과 1/r^2은 Ai에서 상수로 볼 수 있습니다. 그래서 외부 적분은 내부 적분을 |Ai| 배 한 것으로 평가됩니다, 그리고 방정식은 다음과 같이 축소됩니다:

그리고, 물론, 패치 Aj에 대해서도 같은 가정을 만들 수 있습니다. 따라서 적분도 상수취급 될 수 있으며, 근사된 해는 아래와 같습니다:
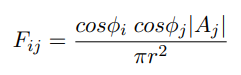
The Hemicube method
비록 우리가 폼팩터 방정식을 단순화 했지만, 패치 대 패치 기반 계산은 여전히 비쌀 것입니다. 따라서, 폼팩터의 계산을 균일하게 만드는 빠른 알고리즘이 고안되었습니다. Bounding Hemisphere를 사용하면, hemisphere의 동일한 영역에 투영된 모든 패치가 같은 폼팩터를 가진다는 것을 알 수 있습니다. 이것은 그림 2(a)에서 보여줍니다, 거기서 4개의 패치 모두 같은 폼팩터를 가집니다.
특히, hemicube의 패치는 알고리즘에서 사용됩니다.
옆면 1 unit 의 Hemicube는 폼팩터가 계산되는 패치 중앙에 위치합니다. Hemicube의 각각의 5면은 Hemicube 픽셀로 불리는 정사각형 패치 집합으로 분할됩니다. 그림 2(b)에 예제에서 각 면은 16개로 쪼개집니다. 여기서 속도와 정확성 사이의 트레이드오프가 있습니다. 더 큰 크기의 hemicube 픽셀일수록, 폼팩터의 평가는 더 나빠질 것입니다, 그러나 더 빠른 알고리즘일 것입니다.
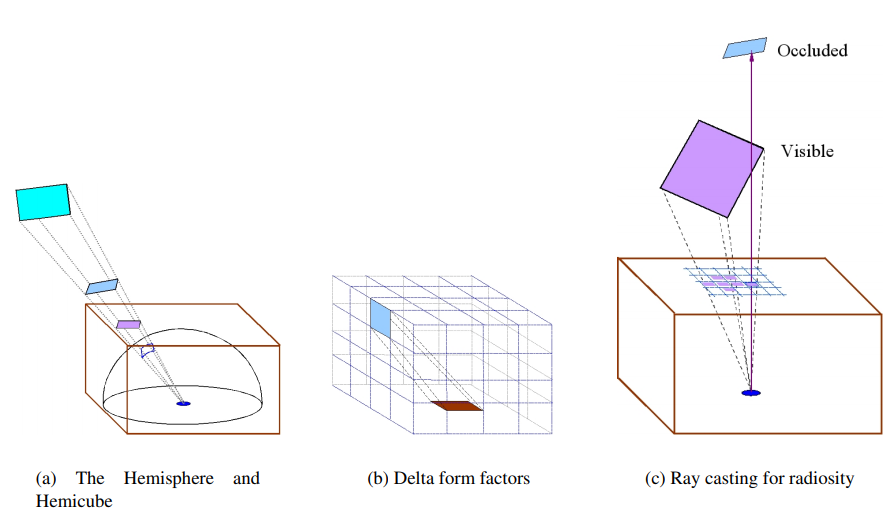
우리고 고려 중인 Hemicube 픽셀과 패치 사이의 폼팩터는, 델타 폼팩터(Delta form factor)라 불림, 우리가 계산하고 있는 패치와 동일 할 것입니다. 게다가 지오메트리가 매우 규칙적이기 때문에 그들을 계산하는 것은 간단할 것입니다. 예를 들어, 그림3에서 보는 것처럼 hemicube 픽셀의 중심을 [xp, yp, 1]이라고 가정합시다. 패치에서 원점으로 향하는 벡터는 단위 벡터이기 때문에 [-xp, -yp, -1]/r로 둘 수 있으며, 여기서 r=sqrt(xp^2 + yp^2 + 1)로 둡니다. 패치의 표면의 단위 노멀은 [0, 0, -1]입니다, 그래서 두 벡터의 내적은 cosφi = 1/r. 비슷한 이유로 cosφj = 1/r 입니다. 만약 hemicube 픽셀의 면적이 ∆A면, 폼팩터는 아래와 같습니다:

그래서 윗면의 델타 폼팩터 방정식은 아래와 같이 주어집니다:

비슷한 이유로 우리는 옆면의 폼팩터를 다음과 같이 추론할 수 있습니다:

그러므로 이런 픽셀들에 대한 값들은 쉽게 계산되고 저장될 수 있습니다, 그리고 비슷하게 hemicube의 옆면의 델타폼팩터를 위한 간단한 방정식이 유도될 수 있습니다.
우리가 이전에 언급한 것 처럼 hemicube의 같은 영역에 투영된 모든 패치는 동일한 폼팩터를 가집니다. 그래서 만약 패치가 정확히 hemicube 픽셀에 투영되면, 그것의 폼팩터는 hemicube 픽셀에 대한 델타 폼펙터와 동일할 것입니다. 만약 패치가 여러 hemicube 픽셀로 투영되면, 그것의 단순히 폼팩터는 hemicube 픽셀의 델타 폼팩터의 합입니다. 우리는 이것을 그림 2(c)와 같은 ray casting 연산을 사용하는 폼팩터에 대한 근사값을 찾는데 활용합니다. 각 hemicube 픽셀에 대해서, 우리는 그것의 중심에서 ray를 발사하고 장면의 또 다른 패치와 충돌한 가장 가까운 지점을 찾습니다. 우리는 이 패치가 hemicube 픽셀로 완전히 투영되며, 다른 모든 패치는 그 패치에 의해 가려진다고 가정합니다. 더 작은 hemicube 픽셀일수록 이렇게 될 가능성이 높습니다, 그리고 더 나은 폼팩터를 평가를 가집니다. ray casting은 ray tracing 강연에서 설명된 기술로 수행될 수 있습니다. 각 hemicube 픽셀에 대해서, 우리가 계산하는 폼팩터의 패치 중심에서 픽셀(역주:hemicube pixel)의 중심을 통해 장면으로 광선을 투사합니다. 우리는 그것과 충돌한 가장 가까운 패치를 찾습니다. 모든 이전의 정교한 방법들은 일관성(to establish coherence)과 ray와 패치의 충돌 계산을 최소화하는 데 사용될 수 있습니다. 우리가 결정할 것은 Hemicube 픽셀에서 어떤 패치가 보이는가 입니다. 우리는 가장 가까운 교차점을 찾은 뒤에 두 번째 ray를 만들 필요는 없습니다.
우리는 폴리곤 렌더링의 대체 수단을 사용하여 같은 계산을 수행할 수 있습니다. 이것을 하기 위해서 장면을 변환해야합니다. 변환된 장면의 원점은 계산중인 패치의 중심입니다, 그리고, hemicube의 윗면의 경우, 그림 2(c)의 수직으로 위쪽으로 바라보는 방향이 면의 중심을 통과합니다. 각 패치 정점(vertex)은 매트릭스의 곱셈으로 윗면에 투영될 수 있습니다, 그리고 투영된 픽셀은 raster filling 알고리즘으로 결정될 수 있습니다. 우리는 hemicube 픽셀에 투영되는 가장 가까운 패치를 찾아야 합니다, 그리고 모든 다른 것들은 가려진 것으로 볼 수 있습니다. 기본적으로 장면을 렌더링 할 때, 숨겨진 부분을 제거할 때와 동일한 선택을 합니다. 우리는 z-buffer를 활용할 수 있을 겁니다, 그리고 이전에 픽셀 할당된 다른 것보다 더 가까운 것이 있다면 픽셀에 패치를 할당합니다. 또는 Painter's 알고리즘을 사용할 수 있습니다, 그래서 패치를 hemicube에 투영하기 전에 거리에 따라 정렬합니다. 특정 픽셀에 할당할 마지막 패치는 다른 모든 픽셀을 대체합니다. 할당 프로세스가 완료되면, 장면의 각 패치의 폼팩터는 그들이 투영되는 hypercube 픽셀의 델타 폼팩터의 합으로 얻어집니다. 만약 패치가 특정 픽셀에 할당되지 않았으면 일반적으로 폼팩터는 0이 됩니다.
요약하자면, Radiosity 방법은 아래와 같습니다:
- 그래픽스 세상을 개별의 패치로 나눔
- hemicube 방법으로 폼팩터를 계산
- 각 패치의 Radiosity 에 대한 매트릭스 방정식 해 얻기
- 각 패치의 코너에서 Radiosity 값의 평균 내기
- 패치의 각 점의 텍스쳐 맵 계산 (연습으로) 또는
- Vewing Window에 투영하고 쉐이딩을 보간한 결과를 렌더링 함.
Radiosity Images
Radiosity의 대부분의 초기 작업은 Cornell University에서 수행되었습니다, 그리고 이미지와 튜토리얼 자료는 그들의 웹사이트에서 찾을 수 있습니다.
http://www.graphics.cornell.edu/online/research/
'Graphics > 참고자료' 카테고리의 다른 글
| [번역] Screen Space Reflections : Implementation and optimization – Part 2 (0) | 2021.01.30 |
|---|---|
| [번역] Screen Space Reflections : Implementation and optimization – Part 1 (0) | 2021.01.28 |
| [번역] To z-prepass or not to z-prepass – Interplay of Light (0) | 2020.12.24 |
| [번역] Global Illumination Using Progressive Refinement Radiosity (0) | 2020.12.19 |
| [번역+설명추가] Spherical Mapping (0) | 2020.11.29 |



