| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- Wavefront
- ue4
- VGPR
- hzb
- vulkan
- ShadowMap
- shader
- texture
- atmospheric
- Graphics
- rendering
- Nanite
- DirectX12
- SIMD
- GPU
- UE5
- optimization
- Study
- forward
- GPU Driven Rendering
- 번역
- deferred
- scalar
- wave
- unrealengine
- Shadow
- scattering
- RayTracing
- DX12
- SGPR
- Today
- Total
RenderLog
[번역] Screen Space Reflections : Implementation and optimization – Part 2 본문
[번역] Screen Space Reflections : Implementation and optimization – Part 2
scahp 2021. 1. 30. 22:35개인 공부용으로 번역한 거라 잘못 번역된 내용이 있을 수 있습니다.
또한 원작자의 동의 없이 올려서 언제든 글이 내려갈 수 있습니다.
출처 : sugulee.wordpress.com/2021/01/19/screen-space-reflections-implementation-and-optimization-part-2-hi-z-tracing-method/
Posted on January 19, 2021 by Sugu Lee
1. Overview
이전 글에서, 선형 추적 방법(Linear tracing method)을 사용하여 Screen Space Reflection을 어떻게 구현하는지 자세히 설명하고 어떻게 몇몇 기술을 사용하여 최적화할 수 있는지 보여줬습니다. 여기에 그 글의 링크가 있습니다.
이 글에서, 정확도를 유지하면서도 선형 추적 방법의 성능보다 더 좋은 다른 추적 방법을 소개하고 싶습니다. 이 방법은 ‘Hi-Z Tracing’ 방법이라 부릅니다.
이 방법은 ‘GPU PRO 5’의 ‘Hi-Z Screen-Space Cone-Traced Reflections by Yasin Uludag’에서 처음 소개되었습니다. 나는 이 책을 수년전에 샀고 이 챕터를 읽었지만, 나는 최근 까지 그것을 구현해보지 않았습니다.
좋아요. 만약 이 기술의 설명을 위한 책이 이미 있다면, 내가 이 글을 쓰는 목적은 뭘까요?
첫째로, 책은 이 기술을 완전히 설명하지 않습니다. 전체 소스를 제공하지 않습니다. 본문 소스코드는 제공되지만 본문에서 부르는 함수는 제공되지 않습니다. 심지어 본문 코드는 몇몇 오타가 있습니다. 그리고, 책은 이런 미제공 함수를 구현할 명령어를 제공하지 않습니다. 제공되지 않은 모든 부분은 독자들의 몫입니다. 그래서, 이글에서, 나는 이 기술을 어떻게 구현할 수 있을지에 대한 전체 상세 내용을 제공하려 합니다. 또한, 내 구현의 전체 소스코드를 여기에서 제공하고 있습니다.
둘째로, 책에서 설명된 방법은 몇가지 제한이 있습니다. 먼저, 화면의 해상도가 2의 승수에서만 동작합니다. 대부분의 비디오게임 해상도는 1920x1080과 같이 2의 승수가 아닙니다. 그래서, 이 기술은 2의 승수가 아닌 해상도를 사용하면 쓸모없습니다. 다음으로, 반사 반직선의 방향에 따라서 이 방법의 정확도가 감소하는 것을 발견했습니다. 반직선이 카메라로 부터 멀어지는 경우 잘 작동합니다(다른 말로하면, |dir.z| >> |dir.xy| 경우). 그러나 수평이나 수직 방향으로 이동하면 (다른 말로하면, |dir.xy| >> |dir.z| 경우). 나는 이런 한계를 해결할 솔루션을 찾을 수 있었습니다. 그래서 나는 이것에 대해 이야기 할 것입니다.
셋째로, 나는 이 기술의 멋지다는 것을 발견했습니다. 그래서, 이 글을 써서, 이 기술이 더 많은 사람들에게 퍼지고 언제든 사용 가능할 때 사람들이 활용할 수 있었으면 합니다.
2. Overview of the HI-Z Tracing Method
Hi-Z 추적을 사용하여 향상시키고자 하는 선형 추적 방법의 문제를 보여드리겠습니다. 아래 이미지는 반직선이 선형 추적으로 이동하는 것을 보여줍니다.

충돌 샘플에 도착하기 위해서, 시작 샘플과 충돌 샘플 사이의 모든 샘플에서 멈춰야 하고 Depth를 비교해야 합니다. 그러나, 대부분의 시간동안 반직선은 충돌 없이 빈공간을 이동하는 것을 알 수 있습니다. 그래서, 질문은, 이 빈공간을 빠르게 지나갈 방법이 없을까? 입니다. 답은 Hi-Z 추적입니다.
Hi-Z 추적 방법은 Hi-Z buffer (혹은 텍스쳐) 라고 불리는 가속 구조를 생성합니다. 이 구조는 쿼드트리의 상위 4개 셀의 레벨의 최소(혹은 z축의 방향에 따라서 최대) 값을 하위 레벨로 설정하는 Scene Depth의 쿼드트리 입니다.

전체 해상도에서 1x1 해상도까지 레벨을 생성합니다. 텍스쳐의 mip 레벨을 각 쿼드트리 레벨을 저장하고 접근하는데 사용합니다.
아래의 이미지는 그 구조를 사용하여 Hi-z 추적을 하는 동안 어떻게 보일 건지에 대한 아이디어를 줍니다. 이것을 위의 선형 추적 그림과 비교해보세요.
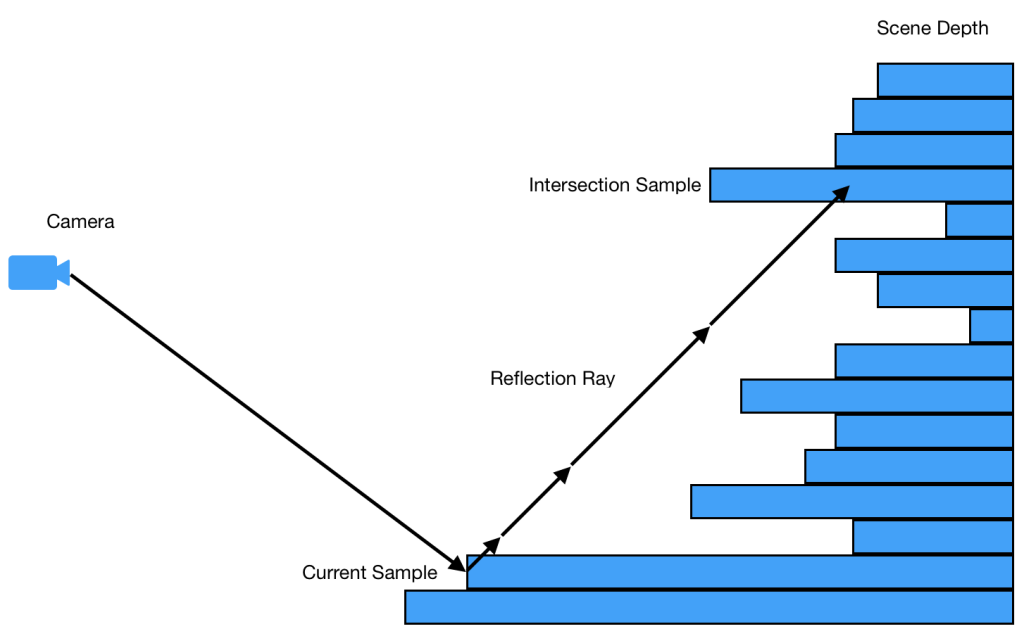
그림에서 보이지는 것 처럼, 충돌 지점에 도착하기 전에 더 적은 샘플에서 멈춥니다. 이것이 이 방법이 선형 추적 방법의 성능을 능가할 수 있는 방법입니다.
보통은, 이 방법은 2 패스로 나뉩니다. 첫번째 패스에서, hi-z 텍스쳐를 Scene Depth 텍스쳐를 사용하여 Base level로 생성합니다. 두번째 패스에서, 이전 패스에서 만든 hi-z 텍스쳐를 사용하여 SSR를 수행합니다.
3. The Hi-Z pass
이 패스에서, 우리는 이후의 SSR에서 사용될 Hi-Z 텍스쳐라 불리는 가속구조를 구성합니다. 이 패스는 여러개의 서브패스로 구성됩니다. 각각의 서브패스는 쿼드트리의 각 레벨을 생성하고 Hi-Z 텍스쳐의 mipmaps에 저장합니다.
첫번째 서브패스는 Scene depth 텍스쳐를 그냥 Hi-Z 텍스쳐의 level 0의 mip 에서 복사하여 Base level을 생성합니다.
그리고나서, 이전 mip level을 입력으로 사용하여 다음 mip level을 생성하는 여러 서브 패스들이 comute kernel을 사용하여 이어서 수행됩니다. 그리고 마지막 mip 1x1 크기가 생성되면 끝납니다. 아래의 다이어그램은 어떻게 서브패스가 동작하는지 설명합니다.

책에 따르면, 아래 레벨의 각 셀은 위 레벨의 최소 2x2로 설정됩니다.

그리고 구현은 아래와 같을 것입니다.
kernel void kernel_createHiZ(texture2d<float, access::read> depth [[ texture(0) ]],
texture2d<float, access::write> outDepth [[ texture(1) ]],
uint2 tid [[thread_position_in_grid]])
{
uint2 vReadCoord = tid<<1;
uint2 vWriteCoord = tid;
float4 depth_samples = float4(
depth.read(vReadCoord).x,
depth.read(vReadCoord + uint2(1,0)).x,
depth.read(vReadCoord + uint2(0,1)).x,
depth.read(vReadCoord + uint2(1,1)).x
);
float min_depth = min(depth_samples.x, min(depth_samples.y, min(depth_samples.z, depth_samples.w)));
outDepth.write(float4(min_depth), vWriteCoord);
}그러나, 이 방법은 위 레벨의 차원이 현재 레벨의 2의 승수인 경우만 가능합니다. 그리고 화면 해상도는 2의 승수가 아닐 수 있습니다. level 0의 차원이 5x5일때, 어떻게 위의 코드가 level 1의 셀을 생성하는지 봅시다.
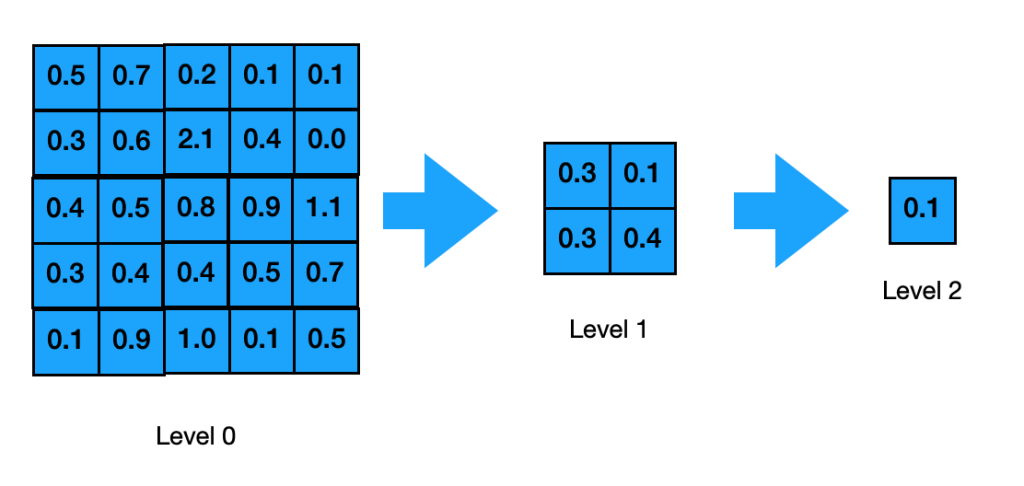
만약 당신이 level 1의 셀을 보고 있다면, 당신은 level 1을 생성할 때, level 0에서 아래쪽과 오른쪽 가장자리의 셀을 가지오지 못하는 것을 알 수 있을 것입니다. 그래서, 명백히, 이 구현은 2의 승수가 아닌 차원에서는 작동하지 않습니다. 그럼, 어떻게 고칠까요?
올바른 해결법을 찾기 위해서, level 1의 각 셀의 범위를 표시한 level 0의 영역을 시각화 해봅시다.

각각의 노란색 박스는 level 1의 범위가 표시된 영역입니다. 이미지에서 볼 수 있는 것 처럼, level 1의 각 셀은 level 0의 2x2 대신 2.5x2.5 셀을 다룹니다.그러므로, 상위 레벨의 차원은 2의 승수가 아닙니다, 셀은 최소 3x3으로 설정되어야 합니다. 그리고, 아래 코드는 수정한 구현을 보여줍니다.
kernel void kernel_createHiZ(texture2d<float, access::read> depth [[ texture(0) ]],
texture2d<float, access::write> outDepth [[ texture(1) ]],
uint2 tid [[thread_position_in_grid]])
{
float2 depth_dim = float2(depth.get_width(), depth.get_height());
float2 out_depth_dim = float2(outDepth.get_width(), outDepth.get_height());
float2 ratio = depth_dim / out_depth_dim;
uint2 vReadCoord = tid<<1;
uint2 vWriteCoord = tid;
float4 depth_samples = float4(
depth.read(vReadCoord).x,
depth.read(vReadCoord + uint2(1,0)).x,
depth.read(vReadCoord + uint2(0,1)).x,
depth.read(vReadCoord + uint2(1,1)).x
);
float min_depth = min(depth_samples.x, min(depth_samples.y, min(depth_samples.z, depth_samples.w)));
bool needExtraSampleX = ratio.x>2;
bool needExtraSampleY = ratio.y>2;
min_depth = needExtraSampleX ? min(min_depth, min(depth.read(vReadCoord + uint2(2,0)).x, depth.read(vReadCoord + uint2(2,1)).x)) : min_depth;
min_depth = needExtraSampleY ? min(min_depth, min(depth.read(vReadCoord + uint2(0,2)).x, depth.read(vReadCoord + uint2(1,2)).x)) : min_depth;
min_depth = (needExtraSampleX && needExtraSampleY) ? min(min_depth, depth.read(vReadCoord + uint2(2,2)).x) : min_depth;
outDepth.write(float4(min_depth), vWriteCoord);
}4. The SSR pass with Hi-Z Tracing
이제 우리는 이전 패스에서 만든 Hi-Z 텍스처를 가지고 있습니다, 이제 우리는 재미있는 부분인 Hi-Z 추적을 사용한 SSR로 갈 수 있습니다.
이 패스를 위해서, 우리는 선형 추적 방법에서 사용한 소스 코드 본문을 그대로 사용 할 수 있습니다. 유일한 차이점은 Scene Depth 텍스쳐 대신 Hi-Z 텍스처를 입력으로 사용하는 것 입니다. 그리고, ‘FindIntersection_Linear’ 대신 ‘FindIntersection_HiZ’를 추적에 사용합니다. 아래는 그 코드 입니다.
kernel void kernel_screen_space_reflection_hi_z(texture2d<float, access::sample> tex_normal_refl_mask [[texture(0)]],
texture2d<float, access::sample> tex_hi_z [[texture(1)]],
texture2d<float, access::sample> tex_scene_color [[texture(2)]],
texture2d<float, access::write> tex_output [[texture(3)]],
const constant SceneInfo& sceneInfo [[buffer(0)]],
uint2 tid [[thread_position_in_grid]])
{
float4 finalColor = 0;
float4 NormalAndReflectionMask = tex_normal_refl_mask.read(tid);
float4 color = tex_scene_color.read(tid);
float4 normalInWS = float4(normalize(NormalAndReflectionMask.xyz), 0);
float3 normal = (sceneInfo.ViewMat * normalInWS).xyz;
float reflection_mask = NormalAndReflectionMask.w;
float4 skyColor = float4(0,0,1,1);
float4 reflectionColor = 0;
if(reflection_mask != 0)
{
reflectionColor = skyColor;
float3 samplePosInTS = 0;
float3 vReflDirInTS = 0;
float maxTraceDistance = 0;
// Compute the position, the reflection vector, maxTraceDistance of this sample in texture space.
ComputePosAndReflection(tid, sceneInfo, normal, tex_hi_z, samplePosInTS, vReflDirInTS, maxTraceDistance);
// Find intersection in texture space by tracing the reflection ray
float3 intersection = 0;
float intensity = FindIntersection_HiZ(samplePosInTS, vReflDirInTS, maxTraceDistance, tex_hi_z, sceneInfo, intersection);
// Compute reflection color if intersected
reflectionColor = ComputeReflectedColor(intensity,intersection, skyColor, tex_scene_color);
}
// Add the reflection color to the color of the sample.
finalColor = color + reflectionColor;
tex_output.write(finalColor, tid);
}나는 선형 추적에 대해서 이전글에서 이미 이 코드의 부분에 대해 이야기 했습니다. 그래서, 이 부분을 넘기고 Hi-Z 추적을 사용하여 충돌지점을 찾는 ‘FindIntersection_HiZ’ 함수로 갑시다.
float FindIntersection_HiZ(float3 samplePosInTS,
float3 vReflDirInTS,
float maxTraceDistance,
texture2d<float, access::sample> tex_hi_z,
const constant SceneInfo& sceneInfo,
thread float3& intersection)
{
const int maxLevel = tex_hi_z.get_num_mip_levels()-1;
float2 crossStep = float2(vReflDirInTS.x>=0 ? 1 : -1, vReflDirInTS.y>=0 ? 1 : -1);
float2 crossOffset = crossStep / sceneInfo.ViewSize / 128;
crossStep = saturate(crossStep);
float3 ray = samplePosInTS.xyz;
float minZ = ray.z;
float maxZ = ray.z + vReflDirInTS.z * maxTraceDistance;
float deltaZ = (maxZ - minZ);
float3 o = ray;
float3 d = vReflDirInTS * maxTraceDistance;
int startLevel = 2;
int stopLevel = 0;
float2 startCellCount = getCellCount(startLevel, tex_hi_z);
float2 rayCell = getCell(ray.xy, startCellCount);
ray = intersectCellBoundary(o, d, rayCell, startCellCount, crossStep, crossOffset*64);
int level = startLevel;
uint iter = 0;
bool isBackwardRay = vReflDirInTS.z<0;
float rayDir = isBackwardRay ? -1 : 1;
while(level >=stopLevel && ray.z*rayDir <= maxZ*rayDir && iter<sceneInfo.maxIteration)
{
const float2 cellCount = getCellCount(level, tex_hi_z);
const float2 oldCellIdx = getCell(ray.xy, cellCount);
float cell_minZ = getMinimumDepthPlane((oldCellIdx+0.5f)/cellCount, level, tex_hi_z);
float3 tmpRay = ((cell_minZ > ray.z) && !isBackwardRay) ? intersectDepthPlane(o, d, (cell_minZ - minZ)/deltaZ) : ray;
const float2 newCellIdx = getCell(tmpRay.xy, cellCount);
float thickness = level == 0 ? (ray.z - cell_minZ) : 0;
bool crossed = (isBackwardRay && (cell_minZ > ray.z)) || (thickness>(MAX_THICKNESS)) || crossedCellBoundary(oldCellIdx, newCellIdx);
ray = crossed ? intersectCellBoundary(o, d, oldCellIdx, cellCount, crossStep, crossOffset) : tmpRay;
level = crossed ? min((float)maxLevel, level + 1.0f) : level-1;
++iter;
}
bool intersected = (level < stopLevel);
intersection = ray;
float intensity = intersected ? 1 : 0;
return intensity;
}이 부분이 추적함수의 본문입니다. 선형 추적 방법보다 많이 복잡하진 않죠?
각 섹션으로 가봅시다.
const int maxLevel = tex_hi_z.get_num_mip_levels()-1; float2 crossStep = float2(vReflDirInTS.x>=0 ? 1 : -1, vReflDirInTS.y>=0 ? 1 : -1); float2 crossOffset = crossStep / sceneInfo.ViewSize / 128; crossStep = saturate(crossStep);
여기서, Hi-Z 텍스쳐에서 마지막 mip level인 maxLevel로 설정합니다.
다음으로, 2개의 변수 ‘crossStep’와 ‘crossOffset’를 설정합니다. 두 변수는 쿼드트리의 격자(Grid)의 다음 셀로 반직선을 이동하는데 사용됩니다. 여기서, 내 코드의 ‘crossOffset’ 설정 부분은 책과는 조금 다릅니다. 책에서는, ‘crossOffset’를 아래 코드로 설정합니다.
crossOffset.xy = crossStep.xy * HIZ_CROSS_EPILSON.xy;
거의 내 코드와 같습니다만 책은 어떻게 정확한 ‘HIZ_CROSS_EPILSON’를 얻는지에 대한 설명을 완전히 빠뜨렸습니다. 그래서 내 계산 방법을 사용하였습니다. ‘crossOffset’는 반직선이 셀을 가로지른(Cell crossing) 후에 다음 셀에 들어가도록 반직선을 아주 적은 양의 거리만큼 이동시키는데 사용합니다(Cell crossimg에 관해서는 다음에 알아볼 것입니다). 내 생각에 ‘sceneInfo.ViewSize / 128’는 이런 목적에 맞는 적당한 값이라고 생각합니다.
float3 ray = samplePosInTS.xyz; float minZ = ray.z; float maxZ = ray.z + vReflDirInTS.z * maxTraceDistance; float deltaZ = (maxZ - minZ);
다음 부분에서, 반직선을 Texture space에서의 현재 샘플의 위치로 초기화합니다. 그리고 나서, 반직선의 Z축 방향의 최소와 최대 위치인 ‘minZ’와 ‘maxZ’를 설정합니다. 이것은 우리가 z축에서 반직선이 추적할 범위입니다. 그런뒤, ‘deltaZ’가 minZ와 maxZ 사이의 거리가 되도록 설정합니다.
float3 o = ray; float3 d = vReflDirInTS * maxTraceDistance;
다음으로, ‘o’와 ‘d’를 설정합니다. 이 부분은 내 코드와 책이 다른 또하나의 지점 입니다. 두 변수 ‘o’와 ‘d’는 Depth할 파라메터로 사용하여 반사 반직선의 위치를 파라메터화 하는데 사용됩니다.
먼저 책에서 이것을 파라메터화 하는 것을 봅시다. 그리고 나는 이 방법의 문제를 설명하고 내 해결방법을 설명할 것입니다.
책에서, ‘o’는 카메라의 Near plane의 위치인 z 컴포넌트가 0인 곳에서 반사 방향을 따라 설정합니다. 그리고, ‘d’가 ‘o’에 더해졌을 때, ‘o’가 반사방향을 따라 이동하여 카메라의 Far plane의 위치인 z 컴포넌트가 1인 곳으로 이동하는 값으로 설정합니다. 아래 이미지는 이 아이디어를 보여줍니다.
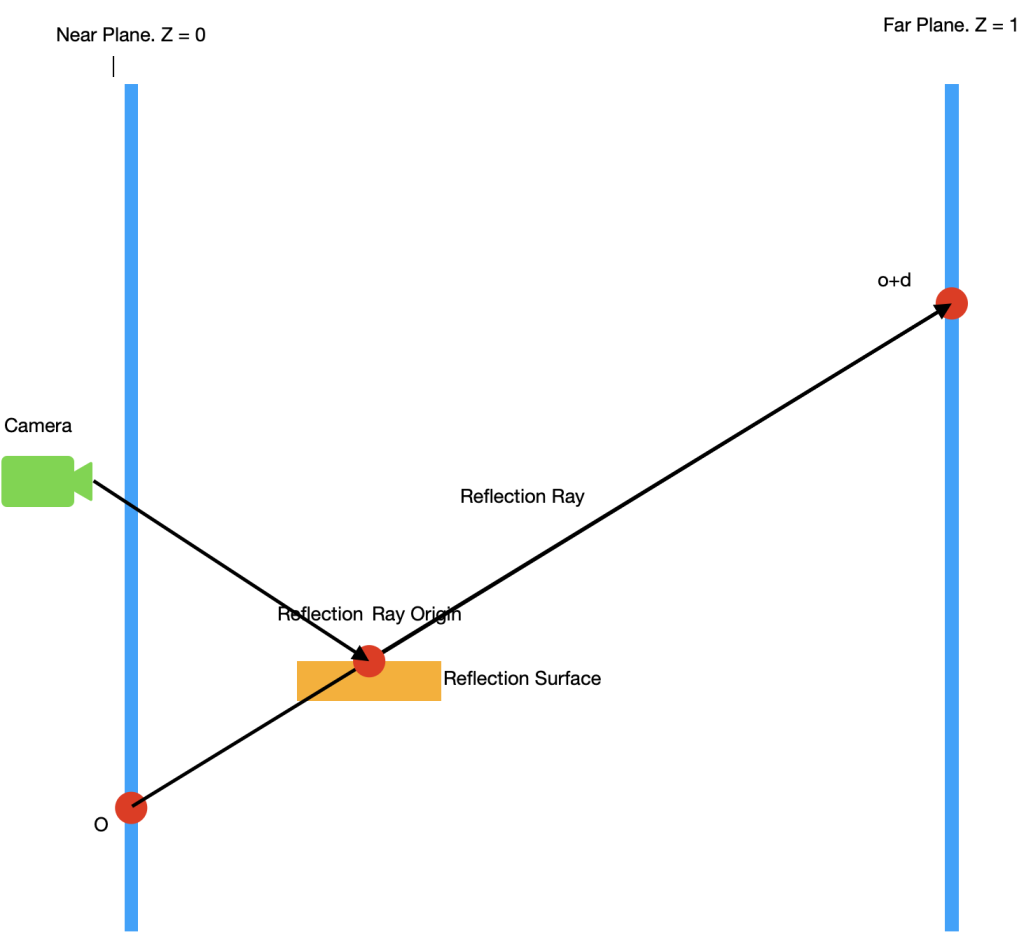
o와 d를 사용하여, 우리는 Depth를 파라메터로 사용하여 반직선을 따라 위치를 얻기 위해서 아래의 식을 사용할 수 있습니다.
ray(depth) = o + d * depth
이 식을 사용하여, Depth가 0일때, 반직선은 ‘o’이 되고 Depth가 1일 때, 반직선은 (o+d)가 됩니다. 반직선의 원점을 얻기 위해, 우리는 반직선의 원점에 Depth를 연결해야 합니다(다른 말로, 현재 샘플의 Depth).
그럼, 이 접근의 문제가 뭔가요? 문제는 반사 반직선의 방향에 따라서, z 컴포넌트가 항상 0과 1이면, ‘o’와 ‘d’의 xy 컴포넌트는 정말 정말 많이 이동할 수 있습니다(양수나 음수). 그리고, 이것은 32 비트 float 숫자 표현을 사용할때, 정밀도 문제를 유발합니다. 아래의 이미지의 예제를 보세요.
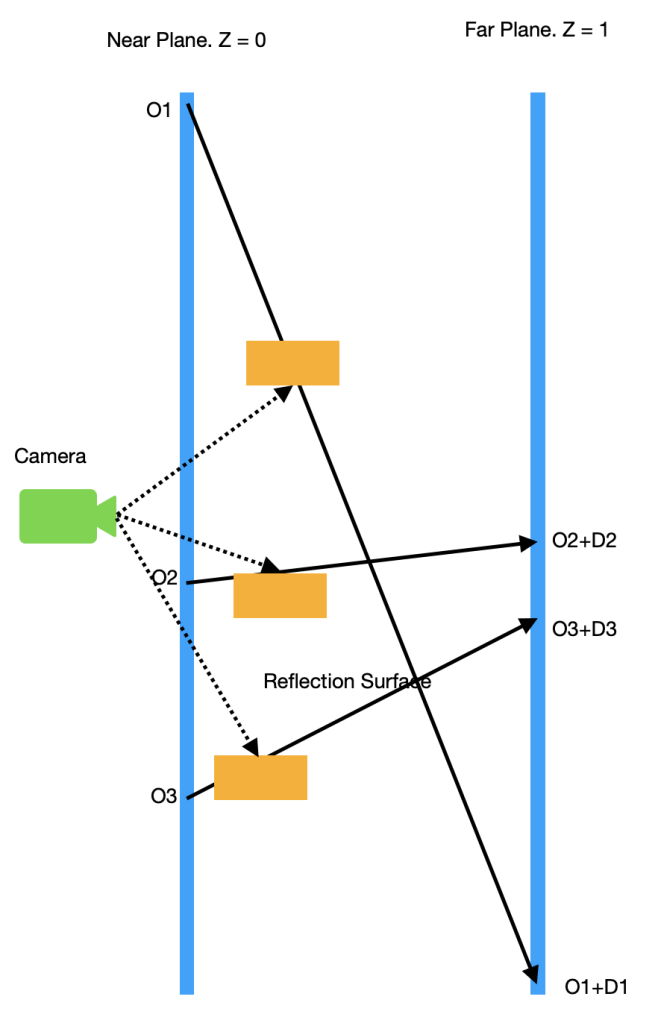
이 예제에서, 우리는 반사 방향의 x나 y 컴포넌트가 z 컴포넌트 보다 큰 것을 볼 수 있습니다. ‘o’의 위치는 View의 중심으로 부터 더 멀어지고 ‘d’의 길이는 길어집니다. 이것이 ‘o’와 ‘d’의 크기를 증가시킵니다.
정밀도 문제를 최소화 하기 위해 ‘o’와 ‘d’의 크기를 가능한 작게 유지하는 것은 아주 중요합니다.
첫째로, 나는 ‘o’가 반직선의 원점에 위치하게 할 것입니다. 왜냐하면 우리는 반직선 뒤를 추적할 수 없을 것이기 때문입니다.
둘째로, 나는 ‘d’를 최대 추적 지점이 가시경계(Visible boundary)를 넘어가기 바로 전의 위치가 되도록 설정하려 합니다. 우리는 반직선이 가시경계를 벗어난 뒤는 반직선을 추척할 필요가 없기 때문에 좋습니다. 우리는 이미 이 위치를 계산했습니다. 그리고 그 위치는 ‘maxTraceDistance’에 반직선의 원점에서 최대 추적 지점까지의 거리로 저장되어있습니다.
이 해결법으로, 위의 예제는 이렇게 바뀝니다.

이 해결법으로, o와 d의 xyz 컴포넌트의 크기는 결코 1을 초과하지 않을 것 입니다. 그리고, 이것은 이후의 식에서 정밀도 문제를 최소화 할 것입니다.
좋아요. 다음 섹션으로 이동합시다.
int startLevel = 2; int stopLevel = 0;
여기서, 우리는 ‘startLevel’와 ‘stopLevel’를 설정합니다. startLevel는 반직선 추적을 시작할 Hi-Z 쿼드트리의 level 입니다. stopLevel는 현재 레벨이 stopLevel보다 더 클때 반직선 추적을 멈출 Hi-Z 쿼드트리의 level 입니다. 우리는 이 숫자를 이어지는 섹션에서 어떻게 사용하는지 볼 것입니다.
float2 startCellCount = getCellCount(startLevel, tex_hi_z); float2 rayCell = getCell(ray.xy, startCellCount); ray = intersectCellBoundary(o, d, rayCell, startCellCount, crossStep, crossOffset*64, minZ, maxZ);
이 코드 섹션에서, 목표는 반직선을 ‘현재 위치에서의 충돌(self-intersection)’을 피하며 반사 방향에 있는 다음 셀로 이동하는 것입니다.
‘getCellCount’ 함수는 주어진 level의 쿼드트리에서 셀의 수를 돌려줍니다. 구현은 아래와 같습니다.
float2 getCellCount(int mipLevel, texture2d<float, access::sample> tex_hi_z)
{
return float2(tex_hi_z.get_width(mipLevel) ,tex_hi_z.get_height(mipLevel));
}그리고, 셀의 수는 특정 mip level의 Hi-Z 텍스쳐의 해상도 입니다. 여기서 mip level은 쿼드트리 level과 일치합니다.
‘getCell’ 함수는 주어진 2D 위치를 포함하는 셀의 2D 정수 인덱스를 돌려줍니다. 이 함수는 ‘pos’와 ‘cell_count’를 입력으로 받습니다. ‘pos’는 찾고 있은 셀의 위치입니다. ‘cell_count’는 찾는 셀의 쿼드트리 level의 너비와 높이입니다. 코드는 아래와 같습니다.
float2 getCell(float2 pos, float2 cell_count)
{
return float2(floor(pos*cell_count));
}getCellCount()를 사용하면, 우리는 시작 level의 쿼드트리 셀 개수를 얻을 수 있습니다, 우리는 시작 level의 쿼드트리에서 현재 반직선의 셀 인덱스를 얻기위해 getCell를 호출 할 수 있습니다.
이제, 우리는 반직선이 위치한 현재 셀 인덱스를 갖고 있습니다. 다음으로, 우리는 반직선을 현재 셀의 바로 다음으로 밀어내기 위해서 ‘intersectCellBoundary’를 사용할 것입니다. 이후에, 반직선은 다음 셀에 있을 것이지만 여전히 현재와 다음 셀 사이의 경계에 가까울 것입니다. 아래의 이미지는 이 함수가 무엇을 하는지 보여줍니다.

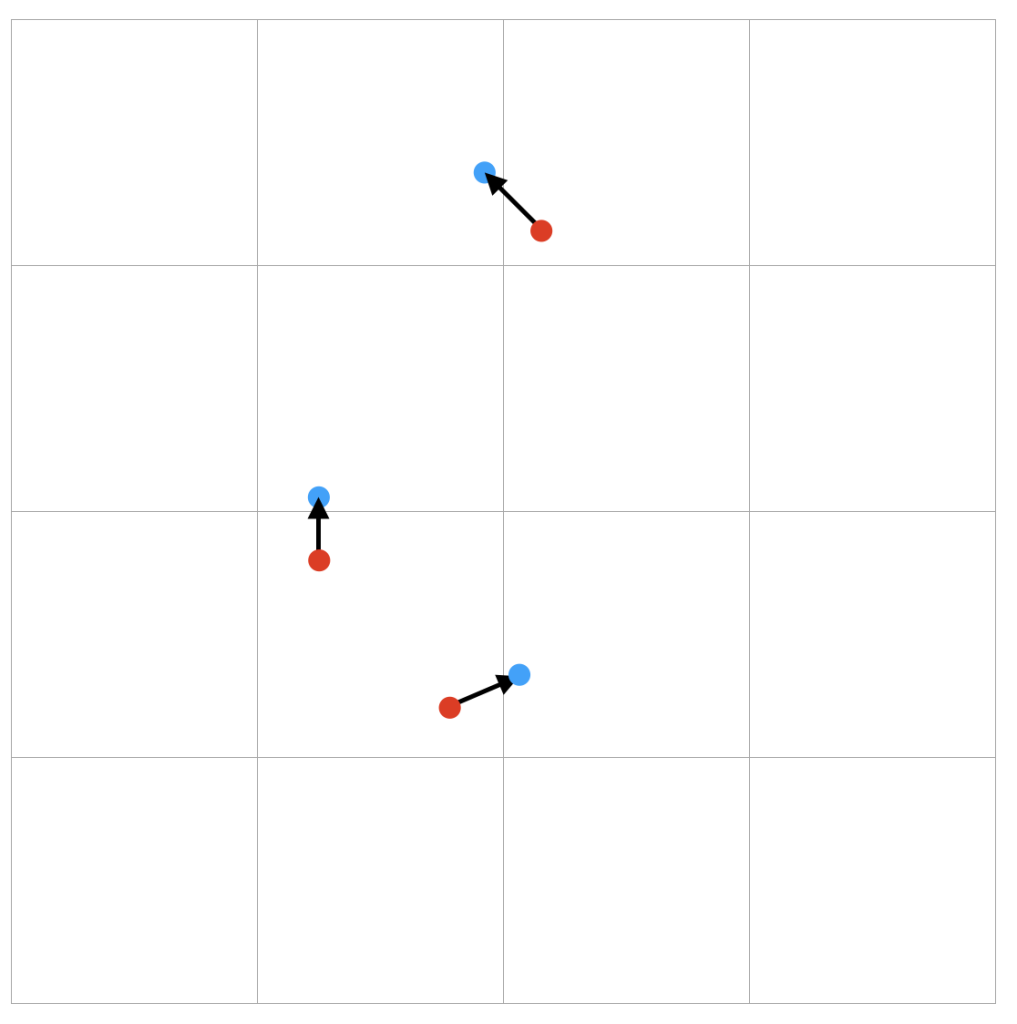
빨간점은 현재위치를 나타냅니다. 그리고, 파란점은 ‘intersectCellBoundary’를 사용하여 계산한 새로운 위치를 나타냅니다. 화살표는 반사 반직선의 방향을 나타냅니다.
아래 코드는 그 함수에 대한 코드입니다.
float3 intersectCellBoundary(float3 o, float3 d, float2 cell, float2 cell_count, float2 crossStep, float2 crossOffset)
{
float3 intersection = 0;
float2 index = cell + crossStep;
float2 boundary = index / cell_count;
boundary += crossOffset;
float2 delta = boundary - o.xy;
delta /= d.xy;
float t = min(delta.x, delta.y);
intersection = intersectDepthPlane(o, d, t);
return intersection;
}이 함수는 crossStep 와 crossOffset 이 사용되는 곳입니다. crossStep는 다음 셀의 인덱스를 얻기 위해서 현재 셀에 추가 됩니다. 셀의 인덱스를 셀의 수로 나눠서, 우리는 현재 셀과 새로운 셀 사이의 경계 위치를 얻을 수 있습니다. 그리고 나서, 새 위치가 경계에 걸쳐있지 않게 하기 위해서 crossOffset를 더하여 위치를 약간 더 이동시킵니다.
그리고나서 새위치와 원래 위치의 거리차이(delta)를 계산합니다. 이 거리차이는 ‘d’ 벡터의 xy컴포넌트로 나눕니다. 나눈 후, 거리차이의 x와 y 컴포넌트는 0과 1사이 값을 가질 것입니다. 이것은 거리차이 위치가 반직선의 원점에서 얼마나 멀리 떨어져있는지 표현합니다.
그리고나서, 우리는 거리차이의 x와 y 컴포넌트 중 더 작은 것을 선택합니다. 왜냐하면 우리는 가장 가까운 경계를 건너가고 싶기 때문입니다. 그후, 우리는 새로운 위치를 계산하기 의해서 마지막으로 ‘intersectDepthPlane’를 호출합니다.
float3 intersectDepthPlane(float3 o, float3 d, float z)
{
return o + d * z;
}이 함수는 앞서 소개한 반사 반직선이서 위치를 계산하기 위해 파라메터화되어진 형태입니다.
어쨌든, 책에서 시작위치에서 다음 셀로 밀어내는 코드는 이것 입니다.
ray = intersectCellBoundary(o, d, rayCell, startCellCount, crossStep, crossOffset);
책의 코드와 내 구현 중 오직 다른점은 내 구현은 intersectCellBoundary를 호출 할때, ‘crossOffset’에 64를 곱하는 것입니다. 이것을 곱해주는 것은 화면 해상도가 2의 승수가 아닌 경우 반직선을 다음 셀로 적절히 밀어내기 위해 필요합니다. 이것이 왜 필요할까요?
64를 곱해주는 부분을 하지 않은 상태에서 startLevel이 0보다 큰경우, 반직선을 다음 셀로 밀어내기 위해서 ‘intersectCellBoundary’를 호출하는 것은 start level에서 반직선을 다음 셀로 이동시킬 수 있습니다만 start level 보다 높은 레벨에서는 그렇지 않습니다. 아래의 예를 보세요.

초록색 셀 level은 5x5 입니다. 검은색 셀 level은 2x2 입니다. 두 위치는 다음 셀로 이동합니다.위쪽에 있는 것은 잘 동작하는 반면에 가운데 있는 것은 그렇지 않습니다. 위치가 2x2 level의 다음 셀로 이동했습니다. 그러나, 그것이 5x5 다음 셀로 이동하는 것은 실패했습니다. 이 문제는 화면 해상도가 2의 승수인 경우 발생하지 않습니다.
더 큰 crossOffset를 사용하는 것은 경계로부터 위치를 더 많이 이동시켜서 이 문제를 해결할 수 있습니다. 이것이 내가 crossOffset에 64를 곱한 이유입니다.
좋습니다. 이제, 우리는 실제로 반직선을 추적하는 다음 부분으로 넘어갈 수 있습니다.
int level = startLevel;
uint iter = 0;
while(level >=stopLevel && ray.z <= maxZ && iter<sceneInfo.maxIteration)
{
const float2 cellCount = getCellCount(level, tex_hi_z);
const float2 oldCellIdx = getCell(ray.xy, cellCount);
float cell_minZ = getMinimumDepthPlane((oldCellIdx+0.5f)/cellCount, level, tex_hi_z);
float3 tmpRay = cell_minZ > ray.z ? intersectDepthPlane(o, d, (cell_minZ - minZ)/deltaZ) : ray;
const float2 newCellIdx = getCell(tmpRay.xy, cellCount);
float thickness = level == 0 ? (ray.z - cell_minZ) : 0;
bool crossed = thickness>MAX_THICKNESS || crossedCellBoundary(oldCellIdx, newCellIdx);
ray = crossed ? intersectCellBoundary(o, d, oldCellIdx, cellCount, crossStep, crossOffset) : tmpRay;
level = crossed ? min((float)maxLevel, level + 1.0f) : level-1;
++iter;
}무엇을 하는 것인지 알아보기 위해서 코드를 따라가봅시다.
첫째로, while 반복문으로 시작합니다. 탈출 조건은 현재 level이 stop level 보다 더 큰 경우나 반직선의 z 위치가 maxZ를 넘어선 경우입니다. 우리는 또한 ‘maxIteration’으로 반복 횟수를 제한합니다.
반복문에서, 먼저, 현재 level의 셀 수를 얻습니다. 그리고나서, 현재 level에서 현재 반직선의 셀 인덱스를 얻습니다.
그리고나서, 아래에 구현된 ‘getMinimumDepthPlane’를 사용하여 현재 쿼드트리 level 에서 현재 셀의 최소 깊이 값을 얻습니다.
float getMinimumDepthPlane(float2 p, int mipLevel, texture2d<float, access::sample> tex_hi_z)
{
constexpr sampler pointSampler(mip_filter::nearest);
return tex_hi_z.sample(pointSampler, p, level(mipLevel)).x;
}주어진 mip level과 주어진 샘플 위치에서 Hi-Z 텍스쳐를 샘플링 하는 함수입니다.
그리고, 여기가 내 구현이 책과 조금 다른 부분입니다. 아래는 책에 나오는 코드입니다.
float minZ = getMinimumDepthplane(ray.xy, level, rootLevel);
책에서는 ‘getMinimumDepthplane’이 어떻게 구현되어있는지 제공되지 않습니다. 그래서, 나는 세개의 파라메터가 어떻게 사용되는지 몰랐습니다. 그러나, 만약 내가 맞다면, ‘ray.xy’를 샘플링할 좌표 그리고 ‘level’을 mip level로 사용했을 것입니다. 그리고, 나는 ‘rootLevel’이 어떻게 쓰일지는 모르겠습니다.
그래서, 처음에, 나는 ‘ray.xy’를 텍스쳐에서 샘플링하는데 사용해보려 했습니다. 그러나, 가끔 텍스쳐에서 정확하지 않은 위치가 샘플링되는 결과가 있다는 것을 발견했습니다. 내 추측으로는 ‘ray.xy’가 바로 두 샘플들 사이의 경계에 놓여있어서 운이 좋지 않을때는 잘못된 쪽의 샘플을 얻었기 때문이라 생각했습니다.
그래서, ray.xy를 샘플링 좌표로 사용하는 대신, 나는 cellIndex를 현재 셀의 중심의 위치를 계산하는데 사용했습니다. 그리고나서, 나는 그 위치를 텍스쳐로 부터 샘플링하는데 사용했습니다. 그리고 나는 잘못된 샘플링 문제를 완벽하게 해결하였습니다.
좋아요. 현재 셀의 최소의 Depth가 ‘getMinimumDepthPlane’를 사용하여 얻어지면, 우리는 min depth와 반직선의 현재 depth와 비교해야합니다. 비교에는 2가지 결과가 있을 수 있습니다.
A. 현재 depth ≥ min depth : 이것은 반직선이 현재 셀의 볼륨내에 위치한다는 의미입니다. 만약 현재 level이 첫 level이라면, 그러면 우리는 충돌지점을 찾은 것입니다. 그러나, 만약 현재 level이 첫 level이 아니라면, 우리는 반직선이 실제로 충돌 했는지 아닌지 알수 없습니다. 그것을 결정하기 위해서, 우리는 첫 level 까지 돌아가야 합니다.
B. 현재 depth < min depth : 이것은 반직선이 현재 셀의 볼륨 외부에 있다는 의미입니다. 이경우, 우리는 반직선을 새로운 위치의 z 가 min depth가 되는 곳으로 더 멀리 이동할 수 있습니다.

그리고, 이것이 아래의 코드가 하는 것입니다.
float3 tmpRay = cell_minZ > ray.z ? intersectDepthPlane(o, d, (cell_minZ - minZ)/deltaZ) : ray;
심지어 반직선이 더 멀리이동한 경우에도 새로운 위치는 임시 변수에 저장됩니다. 새로운 위치가 현재 셀의 범위내에 있지 않으면 새위치를 재계산 해야하기 때문입니다.
그리고, 그것이 코드의 다음 라인이 하는 것입니다.
새위치의 셀인덱스가 현재 셀인덱스와 동일한지 확인합니다. 만약 그렇지 않다면, 새로운 위치는 현재 위치와 다른 위치에 있다는 것입니다. 이 경우, 새로운 위치를 그대로 사용하는 대신에, 우리는 현재 반직선을 이동해 다음 셀의 위치를 얻기 위해서 ‘intersectCellBoundary’를 사용합니다.
우리는 또한 ‘MAX_THICKNESS’ 보다 두께가 더 두꺼울 때 반직선은 다음 셀로 이동합니다. 이것이 반직선이 오브젝트를 통과해서 넘어간 경우를 허용하는 방법입니다. 이것은 현재 level 이 0인 경우만 허용해야합니다. 그렇지 않으면, 우리는 예상치 못한 결과를 얻을 것입니다.
그리고, 만약 반직선이 다음 셀로 이동했다면, 우리는 쿼드트리의 더 낮은 level로 이동합니다. 만약 그렇지 않다면, 우리는 더 높은 쿼드트리 level로 이동합니다.
아래의 비디오는 이 모든 것이 어떻게 작동하는지 보여줍니다.
검은색 화살표와 초록색 점은 각 반복에서의 반직선의 위치를 표시합니다. 빨간 점으로 된 선과 빨간 점은 각 반복에서의 반직선의 임시 위치를 표시합니다. 초록색 박스는 각 쿼드트리 level에서의 셀을 표시합니다. 이 예제에서는 Start level과 Stop level 둘다 0으로 설정합니다.
좋아요. 이것으로 반복문 부분을 마칩니다.
마지막 부분은 반직선이 충돌했는지 아닌지 여부를 확인하는 것입니다. 이것을 위해, 우리는 ‘level’이 ‘stopLevel’보다 더 큰지 여부를 확인할 수 있습니다.
또한 우리는 ‘충돌지점’ 반직선의 현재 위치로 설정할 수 있습니다.
5. Performance comparisons with linear tracing method.
여기서, 선형 추적 방법과 Hi-Z 추적 방법의 성능 비교를 보여줍니다. 반직선의 추적 반복을 위한 max iteration 수를 다르게 하여 여러가지 비교를 해볼 것입니다. 반복이 멈추는 때는 반복횟수가 최대 반복수를 초과하던가 반직선이 최대 이동 위치에 도달 또는 충돌지점을 찾은 경우 일 것입니다.
| Linear(SSR Pass) | Hi-Z(HiZ Pass + SSR Pass) | |
| MaxIteration = 1000 | 2.33ms | 1.77ms |
| MaxIteration = 300 | 1.3ms | 1.2ms |
| MaxIteration = 100 | 0.7ms | 1ms |
| MaxIteration = 25 | 0.45ms | 0.8ms |
테이블을 보세요, Hi-Z가 MaxIteraion >= 300 에서 더 빠르게 수행되고, MaxIteration < 300 일 때는 선형 추적 방법이 더 빠릅니다. 그러나, 그것은 사실이 아닙니다, 심지어 같은 최대 반복 수 더라도, Hi-Z 방법은 선형 추적 방법보다 훨씬 더 먼 거리를 추적할 수 있습니다. 아래 그림은 최대 반복에 대한 것을 보여줍니다.
A. MaxIteration = 1000

B. MaxIteration = 300

C. MaxIteration = 100

D. MaxIteration = 25

당신이 보듯이, Hi-Z 방법으로 최대 반복 수 100인 경우 결과는 거의 선형 추적 방법으로 1000번 수행한 결과와 동일합니다. 이제, 우리는 Hi-Z 방법이 얼마나 강력한지 알 수 있습니다.
6. Conclusion
이 책의 명령어와 코드 조각으로 시작하여, 내 구현에서 모든 것이 옳바르게 작동하는데는 약간의 노력과 시간이 필요했습니다. 그리고 나는 그것을 한것이 기쁩니다.
내가 말했듯, 책은 이 기술을 어떻게 적절히 구현하는지에 대한 전체 상세정보를 제공하지 않습니다. 그래서, 나는 이 글이 이 기술에 관심이 있고 구현하고자 하는 사람들에 도움이 되길 바랍니다.
읽어주셔서 감사합니다!
'Graphics > 참고자료' 카테고리의 다른 글
| [번역] How to read shader assembly – Interplay of Light (0) | 2021.04.24 |
|---|---|
| [번역] Implementing FXAA (0) | 2021.02.17 |
| [번역] Screen Space Reflections : Implementation and optimization – Part 1 (0) | 2021.01.28 |
| [번역] Lecture 13: Radiosity - Principles (0) | 2020.12.30 |
| [번역] To z-prepass or not to z-prepass – Interplay of Light (0) | 2020.12.24 |




