| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- RayTracing
- rendering
- forward
- 번역
- Nanite
- ue4
- atmospheric
- hzb
- Wavefront
- DirectX12
- VGPR
- texture
- SIMD
- ShadowMap
- Study
- shader
- DX12
- unrealengine
- SGPR
- deferred
- GPU
- Graphics
- vulkan
- wave
- UE5
- scalar
- GPU Driven Rendering
- optimization
- Shadow
- scattering
- Today
- Total
RenderLog
[번역]Radiometry (Steve Marschner, Cornell University) 본문
개인 공부용으로 번역한 거라 잘못 번역된 내용이 있을 수 있습니다.
또한 원작자의 동의 없이 올려서 언제든 글이 내려갈 수 있습니다.
원문 : https://www.cs.cornell.edu/courses/cs6630/2015fa/notes/02radiom.pdf
Radiometry
Steve Marschner
Cornell University
CS 6630 Spring 2012, 26 January
Radiometry는 공간을 흐르는 Radiant energy 를 설명하는 시스템입니다. 이것은 기본적으로는 기하학 주제입니다-모든 세부사항들은 기하학에 있지 빛의 물리학에 있지 않습니다.
우리가 기하학적 광학 모델을 Radiometry에서 사용하기 위해서 많은 가정들이 있습니다:
• visible light (or thereabouts)
• incoherent light
• unpolarized light (random polarization)
• macroscopic scale
이 가정들과 함께하면 우리는 빛의 파동 특성의 볼 수 없을 것입니다-간섭 줄무늬 없음, 회절, 등등. 극성이 없는 빛이라는 제한은 아마도 최소한 유효할 것입니다. 그리고 주로 편의상 만들어졌습니다. 편광을 모든것에 포함하는 것은 우리가 이 과정에서 하는거에는 어렵지 않습니다; 그것은 단지 한다발의 추가적인 bookkeeping 입니다.
기하학적 광학에 알맞는 멘탈 모델은 빛을 입자의 흐름으로 생각하는 것입니다. 마치 한다발의 비비탄이 장면주변을 날아다니는 것 처럼. 각각의 입자(우리는 아마 편하게 광자(Photon) 이라 부를 것임)는 방향과 파장과 연관되어있는 점 입니다. 이 입자들은 모든 방향의 공간으로 같은 속도로 흐릅니다. 각각의 입자는 작은 고정된 양의 에너지를 옮기며, 그들이 어떤것에 부딧치기까지 직선방향으로 이동합니다. 그들은 서로 상호작용하지 않습니다(그들은 서로 방해하지 않습니다).
당신은 카메라 CCD나 인간의 눈을 광자를 모으는 빛검출기로 생각할 수 있습니다. 그래서 궁극적으로 우리가 시뮬레이션 하고싶은 양은 단순히 특정 픽셀에 속하는 입자의 개수 입니다.
이 입자의 수는 에너지의 양을 표현합니다. Radiometry는 다른 공간, 다른 방향 그리고 다른 시간의 영역들의 에너지를 측정하는 것입니다.
여담: Solid angles
Radiometry에서 측정단위 중 눈에 띄는 것 중 하나는 Solid angle 이다. 이것은 2D에서 3D로 각도(angle) 개념이 일반화 된 것이다. 2D에서 방향을 (단위 벡터) 단위원 위의 점으로 생각 할 수 있다. 그리고 3D에서 방향을 단위구 위의 점으로 생각할 수 있다. Solid angle의 정의는 이 두가지 생각의 유사성에 의해 이루어 집니다:
각도는 단위원의 한 조각입니다; 각도의 크기는 그것의 호의 길이 입니다:

Solid angle은 단위구의 한 조각입니다; Solid angle의 크기는 그것의 영역입니다:
방향의 세트를 각도로 하는 아이디어는 아마 새로울 것입니다. 2D의 각도(세트)와 각도의 크기(개수)를 구분하는 것은 좋은 점 입니다. 왜냐하면 세트가 서로 연결되어 있는한 그것은 단지 원위의 간격일 뿐이기 때문입니다. 3D에서, Solid angle의 모양의 질문은 더 흥미롭습니다. 왜냐하면 구 위에 특정 영역이 있는 모든 종류의 영역이 있을 수 있습니다.
2D 기하학에서는 어떠한 다른 점에 대응하는 각도에 관해서 이야기 합니다: 예를 들어, 삼각형 꼭지점에서의 각도는 삼각형의 반대쪽 면의 각도와 대응됩니다. 비슷하게 3D에서 한 오브젝트에 대응되는 Solid angle은 그 물체로 향하는 방향의 세트 입니다.
1. Radiometric units, top down
Joules (J) 단위로 측정 된 Energy Q
- 이것은 당신이 실제로 어떤 탐지기로 측정할 수 있는 것입니다: 얼마나 많은 입자가 그것에 충돌했는지
Power, or flux: P or Φ, watts (W = J∕s)
- 단위시간 당 에너지, P = dQ∕dt
- 동의어: radiant flux, Φ
변하지 않는 상태(그래픽스에서 보통 우리가 가정하는 것)에서 Energy와 Power는 기본적으로 교환가능하다, 그래서 우리는 때때로 그들을 조금은 대강대강 구분합니다. 우리가 어떤 실제 탐지기로 Power 를 측정할때, 어떤 시간 간격(노출)에 걸쳐서 에너지를 포착합니다. 이것은 순간의 Power의 추정치 입니다: 노출에 대한 평균 Power 입니다.
Power는 에너지의 미분 값으로 생각할 수 있습니다: dQ∕dt. Power는 빛이 당신의 검출기에 들어가는 Energy의 증가율 입니다. 비록 나는 이것을 피하려고 하지만, 종종 dQ = P dt 이렇게 쓰여져 있습니다.
실제로 Radiant flux는 Radiometry의 시작점 입니다; 모든 다른 Radiometric 의 양은 Power의 밀도입니다.
Flux area density: irradiance E; radiant exitance M (W∕m2)
- 단위 면적당 Flux, E = dΦ∕dA (표면위의 한점에서 측정됨)
- 동의어: radiosity, B, for radiant exitance
Irradiance는 빛이 표면에 도달하는 것입니다; Radiant exitance는 빛이 표면을 떠나는 것입니다. Radiosity는 Radiant exitance 이지만 모든 방향으로 균일한 Radiance라는 것을 내포합니다. 표면은 실제일 수도 가상일수도 있습니다만 우리가 Irradiance에 대해서 이야기 하려면 표면이 필요합니다.
한 지점에서 Irradiance를 계산하는 몇가지 다른 방법들이 있습니다. Irradiance로 불리는 수량은 단방향입니다, 표면방향의 속성; 이 문제에서 표면이 있다는 생각은 자연스럽습니다. 만약 우리가 어떤 공간에 점 x를 이야기 하고 있다면, 표면의 Normal n과 Irradiance E(x, n)를 n방향으로 향하고 있는 표면의 작은 영역위에 떨어질 Irradiance로 정의하는 방식으로 우리는 그 점에서의 Irradiance에 대해 이야기 할 수 있습니다. 당신은 Irradiance 한쪽면에 떨어지는 입자를 계산하는 작은 탐지기를 생각할 수 있습니다.
공간안에 다른 종류의 Irradiance는 Scalar Irradiance 입니다. 또한 Fluence로 알려져 있습니다. 이것은 작은 구면의 탐지기 위에 한점에 떨어질 단위 면적당 Flux 입니다. Fluence φ(x) 는 x의 이웃을 통과한 모든 입자를 그들이 어느방향으로 이동하는지 고려하지 않고 계산합니다.
때때로 공간에서 더 자연스러운 표면 Irradiance의 변종은 net Irradiance 입니다. (이것은 내가 쓰는 용어임: 나는 이것을 표준적으로 어떻게 부르는지 모름) Net Irradiance는 Irradiance와 같지만 표면의 두면의 입자를 계산합니다. 그리고 입자들이 통과하는 방향에 따라서 양성과 음성 입자로 계산합니다. 당신은 Net Irradiance를 마치 마법처럼 날아다니는 입자를 계산하는 작은 링 모양의 탐지기로 생각할 수 있습니다. 나는 표면의 Normal 방향으로 이동하는 입자들을 양성으로 계산하는 방식을 사용할 것이고 반대로 이동하는 것을 음성으로 계산할 것입니다. 이것은 Net Irradiance ¯E (x,n) 그리고 기존표면의 Irradiance E(x, n)의 관계는 아래와 같다는 의미 입니다.
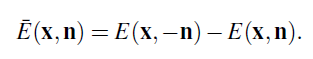
마지막 Irradiance 종류로 우리는 Vector Irradiance를 고려할 것입니다. 이것은 간단히 3개의 컴포넌트가 3개의 축에 대한 Net Irradiance 인 3차원 벡터입니다.
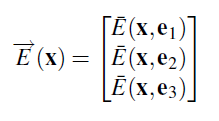
Flux solid angle density: intensity I (W∕sr)
- 단위 Solid angle 당 Flux, I = dΦ∕dω (특정 방향에서 측정됨)
이 개념자체는 Point 형태의 소스에서 대부분 사용됩니다 - 즉, 방출시키는 물체가 너무 작아서 우리는 물체에서 빛이 어디서 부터 나오는지 신경쓰지 않습니다;단지 어느방향으로 가는지만 신경씁니다.
그러나 이것은 특정 작은 오브젝트 위에 빛이 도달하는 것을 설명하는데도 사용할 수 있습니다. 만약 우리가 오브젝트 위의 특정 위치에 도착하는 것이 아닌, 어느 방향으로 부터 빛이 도달하는 총량만 고려한다면요.
Flux 에 대한 Solid angle 그리고 면적: Radiance L (W∕m2sr)
단위 면적당 Solid angle 당 Flux, L = d2Φ∕(dAdω) (표면이나 공간에 특정 위치에 특정 방향에서 측정됨)
L(x, ω) 는 x 주위를 지나면서 ω 주위 방향을 지나가는 광자의 밀도를 측정한 것이다.
"주위"의 세부적인 의미가 이 정의의 핵심입니다-이것은 기하학적인 질문입니다. Radiance는 Radiant flux를 측정합니다. 이 Radiant flux는 우리가 광자를 바라보아 모아진 것이다. 이 광자는 그것의 방향이 ω방향 주위의 Solid angle dw 이고 표면위에 x위치의 dA 면적이 방향 ω에 수직으로 향하고 있는 광자이다.
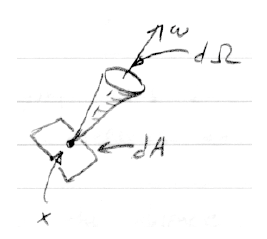
미분 해석: 만약 당신이 dA를 더 크게하거나 dω 를 더 넓게 한다면, 당신은 더 많은 빛을 모을 것이고 L 은 비례의 상수이다.
Radiance는 2차 미분이다: 단위 Solid angle 당 Irradiance 혹은 Radiant exitance 이다. 혹은 단위면적 당 Intensity 이다.

Radiance 불변성
Radiance는 아주 유용하다 왜냐하면 그것은 빈공간에서 직선을 따라서 보존됩니다. 만약 우리가 2개의 점 x1, x2에서 w방향으로 서로서로 바라본다면, 우리는 같은 Radiance를 두 점에서 측정할 수 있습니다. L(x1, ω) = L(x2, ω). 왜이런지 알아보기 위해서, 우리는 각각의 점에서 Radiance를 측정할 수 있습니다. 우리는 이 측정을 우리가 원하는 어떠한 Solid angle 영역들을 사용하여 할수 있습니다. 그래서 w 방향에 수직인 두개의 영역을 dA1과 dA2를 선택해 봅시다.

2개의 Patch를 연결하는 직선 세트를 생각해봅시다 - 두 사각형을 통과하는 직선 세트 임.
dA1와 dA2를 차례로 통과하는 모든 광자는 이 직선 세트를 따라 이동합니다. 각각의 도착점에서 Radiance를 측정하기 위해서 우리는 Solid Angle을 선택해야 합니다. 반대쪽의 표면을 통과하는 모든 방향과 정확히 일치하는 Solid Angle을 고르는 것이 요령입니다. 우리는 dA1에서 dA2로 대응되는 Solid Angle 로서 dω1을 정의합니다. 비슷하게 dω2는 dA2에서 dA1으로 대응되는 Solid Angle 선택합니다. (아마 이 Solid Angle은 표면위의 각각의 점들마다 다를 거라는 것을 눈치 챘을 겁니다. 이것은 작은 영역이라는 제한안에서는 모든 Solid Angle이 동일하기 때문에 괜찮습니다.) Solid Angle의 크기는 아래와 같습니다.
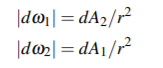
이제 d^2Φ를 두 표면 사이의 flux로 두겠습니다. - 이것은 dA1을 통과한 다음 dA2를 통과하는 모든 입자들이 옮기는 에너지 입니다. 우리가 Radiance 측정을 위해서 Solid Angle을 선택한 방식 때문에 d^2Φ는 양쪽 끝의 Radiance를 측정하는 사용되는 Power 가 됩니다:
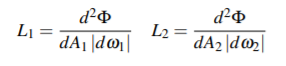
만약 우리가 2개의 Solid Angle의 크기로 표현을 대체한다면, 아래와 같습니다:
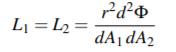
Radiance의 보존은 다음을 의미 합니다. 방해가 되는 어떠한 것이 없는 경우, Radiance는 (점과 방향)의 쌍으로의 속성보다는 공간안에 직선의 속성에 더 가깝습니다.(역주: 반직선인 Ray 보다는 양방으로 무한한 직선의 의미인 Line을 이란 뜻으로 보임) dA1 |dω1| = dA2 |dω2| 으로써 알수있는 점은 Solid Angle 곱하기 면적은 직선 공간의 잘 정의된 척도입니다(역주: dA1 |dω1| = dA2 |dω2|가 L1과 L2 에서 Flux를 나눠주기 때문에 Flux를 계산하는 기준점이 될 수 있는 값이라는 것 같습니다..): 우리는 2개의 다른 위치에서 직선 세트를 측정할 수 있고 같은 답을 얻을 수 있습니다. (마지막의 카메라 예제를 보세요)
투영된 면적과 투영된 Solid angle
우리의 Radiance 의 정의들은 질의한 방향에 수직하는 표면 영역입니다.
우리가 그것과 수직이 되지 않는 다른 표면을 처리해야한다면 어떨까요?
간단한 답변: ω 방향으로 angle θ 만큼 경사진 표면은 같은양의 입자들이 표면에 수직한 ω 방향으로 통과합니다. 그러나 그 표면은 cos θ 만큼 더 작습니다.

우리가 기울어진 표면을 dAʹ라고 부르고 방향에 수직인 표면을 dA라고 한다면, dA = dAʹcos θ입니다. 그리서 Radiance는 아래와 같이 표현할 수 있습니다.
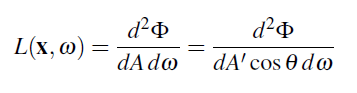
코사인의 존재는 상당히 불편합니다, 그래서 측정 단위 내부에 숨기는 것이 좋습니다.
이것을 할수 있는 2가지는 방법은 다음과 같습니다. (dAʹcos θ)를 그룹 지어주는 것과 그것을 “ω 방향으로 dAʹ에 투영되어진 면적” 또는 (dω cos θ)를 그룹 지어주는 것과 그것을 “투영되어진 Solid angle”이라고 부르는 것입니다.
나는 투영되어진 Solid angle이 아주 편리한 표기 도구라는 것을 찾았습니다. 그래서 나는 이것을 우리의 강좌에서 많이 사용할 것입니다. 평범한 Solid angle은 Sphere 에서의 지정한 특정 측정면적을 측정합니다; 투영되어진 Solid angle은 비슷하지만 Sphere의 적도 부근 영역을 조금 더 적게 계산하는 것이 다릅니다. 그래서 Sphere의 극 위치는 더 많이 계산합니다. 혹은 아래의 Nusselt analog 를 보세요. 나는 종종 Radiance를 투영되어진 단위면적 당 Solid angle 당 Flux로 정의하는 것을 봅니다. (또는 Solid angle 당 투영되어진 으로 쓰기도 함), 그러나 실제로 "투영되어진"이 하는 일은 전파되어지는 방향에 수직한 표면위에서 측정된 면적의 Radiance 입니다.
2. Radiometric units, bottom up
Radiance의 기본 개념(Preisendorfer 는 이것을 "Phase space density" 라 부름)과 모든 다른 것들을 Radiance의 적분으로 생각하는 것으로 부터 우리는 역시 모든 수량을 정의할 수 있습니다.
그것 자체의 정의로 부터, 모든 면적과 Solid angle에 대한 적분을 적용한 Radiance로 부터 Power를 얻을 수 있다는 것은 명확합니다. 예를들어 총 표면 S에 존재하는 총 Power는 다음과 같습니다:
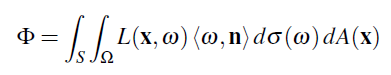
<ω,n>는 ω 에 수직이 아닌 표면을 사용할 수 있게 해주는 코사인 요소 입니다. dσ(ω) 는 다음을 의미합니다. 적분변수(the integration variable)는 ω 이며 우리가 사용하는 측도(the measure)는 σ입니다 , 구의 방향으로 측정한 Solid angle을 내가 부르는 이름. 비슷하게 dA(x)에서 x는 적분변수고 면적은 측도이다. 적분도메인 Ω은 표면 Normal n에 내적을 한 결과가 양수인 결과가 나오는 방향에 해당하는 반구 입니다.(역주 : 그냥 표면의 앞쪽이란 뜻임), 그리고 우리는 ω 방향에 대한 Radiance를 적분 합니다. 왜냐하면 우리는 표면을 떠나고 있는 Radiance에 관심이 있기 때문입니다. L(x,–ω) 을 적분하게 되면 표면위에 들어오는 총 Power를 얻을 수 있습니다.
만약 표면 S가 평평하지 않다면, n은 x의 함수이다, 반구 Ω 도 마찬가지다.
적분의 표기법은 투영되어진 Solid angle을 사용하므로써 간단해질 수 있습니다. 나는 새로운 측도로 ("투영되어진 Solid angle 측도" 라고 불리는 μ) μ를 정의하였습니다. 그것의 연관성을 아주 미소한 세트를 위해 σ 에 줌으로써:
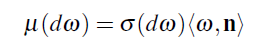
이것에 대해 생각할 수 있는 멋진 기하학적 방법인 “Nusselt analog”가 있습니다: 반구 상의 어떤 세트 D에 대해서, μD는 반구의 기저 평면(역주 : 바닥)에서 D의 그림자의 면적입니다:

투영되어진 Solid angle 측도를 사용하는 것은 아래와 같이 쓸 수 있습니다.
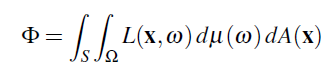
또는
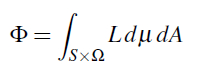
Solid angle 에 대한 적분만 수행하면 Irradiance(–ω) 를 얻거나 Radiant exitance (+ω)를 얻습니다:
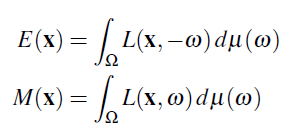
Net irradiance 는 계산하기 쉽습니다: 간단히 전체 Sphere를 적분합니다. 그리고 Radiance가 뒤쪽 방향으로 가는 것에 대해서 마이너스를 제공하기 위해서 내적을 해줍니다.
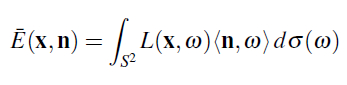
그리고 마지막으로, Vector Irradiance은 이 프레임워크에서 아주 간단한 표현식을 가지는 것으로 이해된다:

여기에 ωi 는 ω의 i 번째 컴포넌트 이다. 그리고 벡터의 양을 적분하면 각각의 3 컴포넌트가 따로 적분되어진 결과를 포함하는 벡터가 됩니다.
Scalar Irradiance는 Irradiance보다 더 간단합니다:
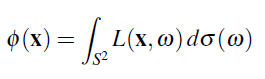
면적에 대해서만 적분하면 Intensity를 얻습니다:
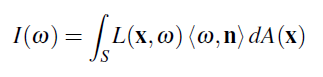
우리는 코사인 요소를 숨겨주는 "투영되어진 면적" 측도를 만들 수 있었습니다. 그러나 이러한 계산은 Irradiance 처럼 그리 흔하지 않기 때문에. 나는 신경쓰지 않을 것입니다.
3. Examples
다양한 수량들을 위한 검출기
이러한 수량들을 위해서, 검출기를 생각해보는 것은 도움이 된다. Flux에 대해서, 검출기 위에 떨어지는 모든 광자를 모으는(Photodiode 같은) 넓은 면적의 검출기를 생각해보자:

Irradiance 에 대해서, 사진 필름 한 조각을 생각해보자. 각각의 점은 그 점에 떨어진 광자의 밀도와 관련있는 신호를 기록한다. 그러나 그것이 어디로부터 왔는지는 신경쓰지 않는다:

디지털 이미지 센서는 아주 작은 flux 계량기 로 비슷한 종류의 측정을 수행한다.
Radiance에 대해서, 전형적인 예제는 카메라는 눈이다. 만약 우리가 이미지의 작은 영역을 본다면 (하나의 픽셀), 그 영역은 어떠한 Solid angle로 부터 렌즈에 도달한 빛을 수집합니다. 카메라의 조리개 작은 영역을 정의합니다. 그래서 그 픽셀의 값은 단위 면적(조리개의 위치의) 당 단위 Solid angle(픽셀의 반직선 방향의) 당 Flux의 추정치 입니다:

완전확산으로 부터의 반사
Lambertian 표면으로 알려져있는 완전확산을 하는 반사체는 입사되는 Irradiance의 0 <= R < 1 비율로 모든 방향으로 균일한 Radiance Lr을 반사하는 표면입니다. (즉, Radiant exitance Mr 은 R X Irradiance Ei):
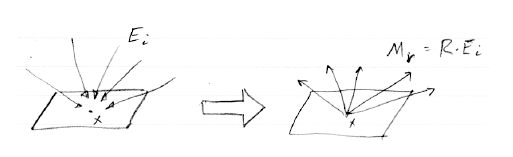
Radiance는 무엇인가요? 우리는 그것이 Radiant exitance M과 연관있는 걸로 알고있습니다:
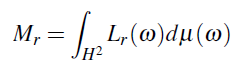
Radiance는 고정되어 있기 때문에, Mr = Lrμ(H^2) = πLr 으로 둘 수 있습니다. (μ(H^2) = π 로 두기 위해서 Nusselt analog 사용)(역주: 반구를 바닥에 투영시킨 경우 평면위의 원의 넓이 영역인 πr^2이므로 단위원이라면 π임)
이것은 아래의 식을 의미합니다.
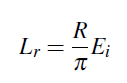
반사되어진 Radiance와 입사되는 Irradiance의 관계는 이후에 BRDF에 대해서 논의할때 다시 나올 것입니다.
카메라에서의 면적과 Solid angle
여기에 Radiance의 불변성에 대한 예제가 있습니다. 1미터 떨어진 벽을 향하는 카메라가 있고 카메라의 조리개는 A1 = 1cm^2 면적을 가지고 있다고 가정해보자. 한개의 픽셀이 면적 A2 = 1 mm^2 에 매핑 된다고 두자. 카메라의 관점으로 부터 픽셀의 Solid angle은 10^(-6) sr 입니다. (Solid angle이 면적/거리의제곱 임을 기억하자). 벽으로 부터, 카메라의 조리개는 10^(-4)sr 의 Solid angle 대응합니다. 만약 벽의 Radiance가 L 이라면, A2로 카메라 조리개를 때리는 Power 는 Φ = L × 10^(–6) m^2 × 10^(–4) sr이다. 카메라에서 Radiance의 측정으로써 이것을 해석하면, 우리는 또다시 Φ ∕ 10^(–4) m^2 ∕ 10^(–6) sr 를 얻을 수 있다.
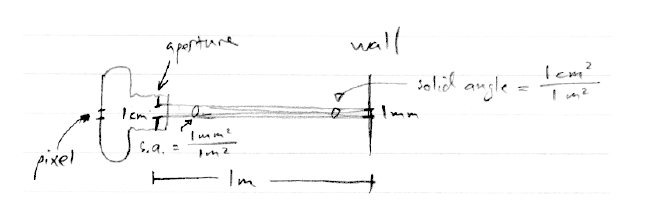
만약 우리가 1km 떨어진 산중턱을 창문을 통해 카메라로 바라보면, 픽셀은 1 m^2 의 면적에 매핑되지만 산으로 부터 카메라의 Solid angle은 10^(-10) sr 입니다. 그리고 만약 산이 벽과 같은 Radiance라면 우리는 카메라로 들어오는 같은 Power 를 얻을 것입니다.

핀홀 카메라에서 Radiance의 감쇄
한 방향으로 작은 구멍이 뚤려있는 박스를 만들었고 필름 한나가 반대면 방향에 있다고 가정해봅시다. 이것이 핀홀 카메라입니다. 만약 우리가 이 카메라를 균일한 Radiance L로 향하게 한다면(예를들면, 흐린하늘), 필름위의 Irradiance는 얼마일까요?
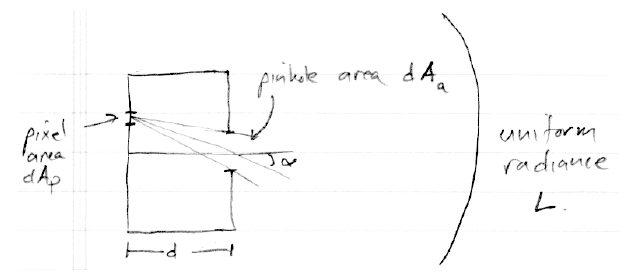
아주 평평한 상자를 생각해보면(상단의 중앙에 핀홀이 있는 셔츠박스를 말함), Irradiance는 균일하지 않다는 것이 명백합니다: 핀홀에 가까울 수록 더 밝아지고 더 멀어질 수록 어두워집니다. 게다가 그것은 방사상 대칭(Radially symmetric)이어야 합니다. 그래서 Irradiance 는 빛이 필름을 때리는 각도 함수입니다; 이것을 α 라 부릅니다. 핀홀로부터 필름까지 떨어진 거리 d라 부르며, 조리개의 면적 dAa라 부릅니다.
만약 우리가 필름위에 있다면, 우리는 조리개에 대응되는 Solid angle로 부터 들어오는 균일한 Radiance를 볼 수 습니다. 이 Solid angle은
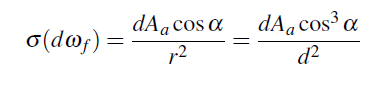
Irradiance는 L 곱하기 μ(dωf) 이며 아래와 같습니다.
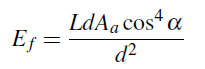
그래서 Irradiance는 조리개의 제곱에 비례합니다(no surprise there), 핀홀 거리의 제곱만큼 줄어듭니다 (no surprise there), 그리고 cos α 의 4승 으로, 이미지의 코너 방향을 향에 줄어듭니다. 이것은 또한 이상적인 렌즈로 만들어진 카메라에도 사실이라고 드러났습니다.
Resolved and unresolved objects in images
우리가 카메라를 물체 방향으로 향했을때, 우리는 물체의 Radiance를 카메라가 기록하는 것으로 생각할 수 있습니다. 만약 우리가 카메라를 물체로 부터 더 가까이 혹은 더 멀리 이동시키면, 그 픽셀의 값이 여전히 같음을 의미합니다. 이것은 Radiance가 픽셀에 일정한 값일때 입니다—즉, 물체가 충분히 픽셀 Grid를 충분히 Resolved 될만큼 크다면:

만약 한픽셀에 물체가 모두 들어갈 수 있게 하기 위해서 물체가 작거나 그리고/또는 멀다면(작은 물방울, 별, 기타 등등), 그때는 조금 다르게 행동합니다. 픽셀값으로 부터의 Radiance를 이야기할 수 없습니다. 그리고 픽셀값은 거리가 달라도 같지 않습니다. 대신에, 그 값은 물체의 Intensity와 관련되어 있습니다, Radiance가 아님, 그리고 그것은 거리의 제곱에 따라 감쇄합니다:

Spherical cap의 Solid angle
각도의 반경 α의 Spherical cap을 고려해봅시다.

그것의 Solid angle은 무엇인가요? 만약 Cap의 중심이 구의 Pole 에 정렬되어 있다면, 이것은 구면좌표계의 간단한 적분 문제입니다:

여기서 나는 그래픽스에 전통적인 구면좌표계를 사용하고 있습니다:θ 는 Pole에서 0에서 시작하여 계산합니다:φ 는 구의 적도 주변을 반시계방향으로 계산합니다.
그림에서 1 – cos α 이 수직축위에 Cap이 투영된 길이라는 것은 흥미롭습니다. 같은 것이 구의 어떠한 밴드 α < θ < β 에도 동작합니다.
\Spherical cap의 투영된 Solid angle은 무엇인가요? 당신은 (sin θ cos θ dθ dφ)을 적분하므로써 그것을 할 수 있습니다, 이것은 어렵지 않습니다.
혹은 당신은 그것을 Nusselt analog로 암산으로 할수도 있습니다. 구의 적도면(바닥)에 투영된 Spherical cap은 반경이 sin θ인 구입니다. 구의 면적은 π sin^2 θ 입니다. 그리고 그것이 Spherical cap의 투영된 Solid angle 입니다.
디스크 모양의 Source의 Irradiance
우리가 디스크 모양의 빛 Source를 가지고 있고, 반경이 R 그리고 일정한양의 Radiance L이라고 가정합시다. 거리 r 에서 Source 방향을 향하는 표면위의 이 Source에 의한 Irradiance 는 얼마일까요?

답은 Source의 Radiance를 x에서 투영된 Solid angle에 대하여 반구 방향의 표면(subtense) 전체 적분입니다. Radiance는 일정하기 때문에, 이것은 L 곱하기 Source에 대응된 Spherical cap의 투영되어진 Solid angle 입니다. 이전 예제의 결과를 사용하여 Irradiance는 아래와 같습니다.

'Graphics > 참고자료' 카테고리의 다른 글
| [번역]Aliasing in computer graphics (0) | 2020.04.10 |
|---|---|
| [번역]Light Indexed Deferred Lighting (0) | 2020.03.23 |
| [번역]Dual paraboloid shadow mapping (2) | 2020.02.15 |
| [번역]Antialiased Deferred Rendering (0) | 2020.02.05 |
| [번역]Hierarchical-Z map based occlusion culling (0) | 2020.01.30 |




