| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- DX12
- wave
- VGPR
- GPU
- 번역
- hzb
- Study
- DirectX12
- rendering
- Shadow
- deferred
- shader
- unrealengine
- scalar
- ue4
- Graphics
- atmospheric
- forward
- optimization
- texture
- UE5
- SGPR
- Nanite
- RayTracing
- scattering
- ShadowMap
- GPU Driven Rendering
- Wavefront
- SIMD
- vulkan
- Today
- Total
RenderLog
[번역]Aliasing in computer graphics 본문
개인 공부용으로 번역한 거라 잘못 번역된 내용이 있을 수 있습니다.
또한 원작자의 동의 없이 올려서 언제든 글이 내려갈 수 있습니다.
출처 : https://apoorvaj.io/aliasing-in-computer-graphics/
컴퓨터 그래픽스를 마주하게 된 대부분의 사람들은 삼각형들을 그릴때 발생하는 보통 jagged edges 라 불리는 앨리어싱을 압니다. 이 글에서는, 3D 그래픽스에서 앨리어싱의 다른 표현을 살펴볼것 입니다, 그리고 이론적으로 그들을 통합할 것입니다. 우리는 앨리어싱을 어떻게 적절히 해결할 것인지 살펴보는것 대신에 그 문제의 원인에만 집중 할 것입니다. 이 글의 다이어그램들과 애니매이션들은 파이썬으로 만들어졌습니다. 나는 공용 도메인에다가 이 코드를 여기서 무료로 받을 수 있도록 하였습니다.
Contents
The Fourier transform
나는 이 글에서 푸리에 트랜스폼을 자세히 설명하지 않을 것입니다. 그것을 이해할 수 있는 직관적인 관점(But what is the Fourier Transform? A visual introduction. by Grant Sanderson) 그리고 공식적인 것(The Scientist and Engineer's Guide to Digital Signal Processing - Chapter 8: The Discrete Fourier Transform by Steven W. Smith) 이렇게 두개의 좋은 자료가 있습니다. 나는 이 책 전체적으로 강하게 추천합니다..
간단히 말해서, 푸리에 트랜스폼은 신호의 시간도메인 표현을 주파수 도메인 표현으로 변환하는 것입니다. 당신은 반대 방향으로 변환하기 위해 푸리에 트랜스폼을 반대로 적용할 수 있습니다.

Sampling vs quantization
샘플링은 보통 균일하게 띄어져있는 시간에서 연속적인 시간 값을 나타냄으로써 이산(개개별의, 별개의) 시간 신호를 얻는 과정입니다. 샘플링은 독립변수(즉, 가로 축-이 경우, 시간)를 연속에서 이산으로 변환합니다.
샘플된 값은 실제 숫자입니다. 당신이 이 값을 디지털로 표현하고 싶을때, 유한한 개수의 비트로 작업합니다. Quantizing은 실제 샘플된 값을 유효한 float 이나 integer로 변환합니다. Quantization은 독립변수(즉, 가로축)를 연속에서 이산으로 변환합니다.
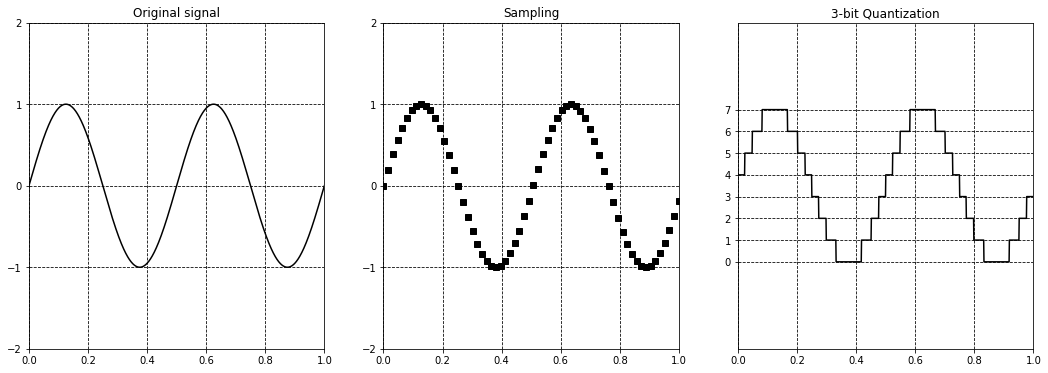
이미지 밴딩은 Quantization에서 발생하는 반면 앨리어싱은 샘플링에서 발생한다는 것을 알아두는 것은 중요합니다.
Proper sampling
앨리어싱을 살펴보기 전에, 적절한 샘플링과 복원(Reconstruction)에 대해 살펴봅시다.
우리는 연속적인 신호 하나를 가집니다-가우시안 펄스 (a). 주파수 도메인 진폭 그림을 (b와 c)에서 나타냅니다. 우리는 피크지점리 0.0 ~0.02 Hz. 인것을 봅니다. (이 글의 모든 예제는 시간 도메인의 실제 값을 사용합니다, 그래서 주파수 도메인 그림은 x축 대칭입니다 x=0).
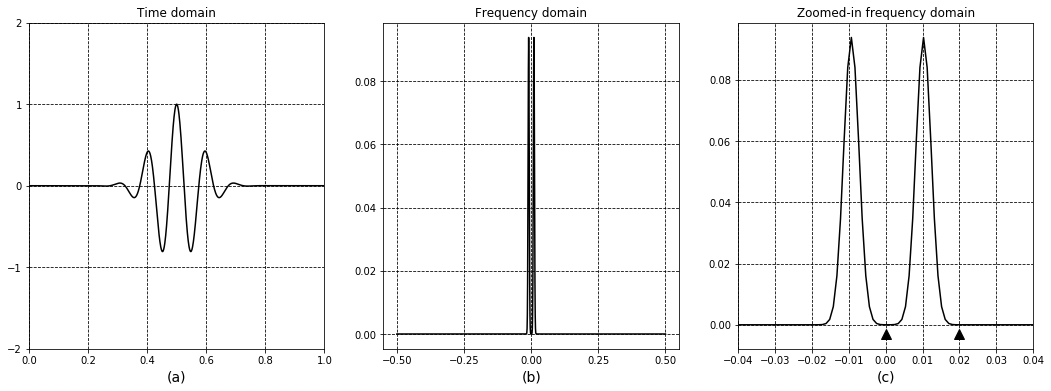
우리는 함수를 어떤 충분히 높은 주파수(이 주파수에 대해서는 곧 더 설명할 것임)에서 샘플합니다, 그리고 우리는 유한한 세트의 이산 값들을 얻습니다. 우리는 이산 점(Point)의 값들로 이 값들이 연속적인 것 처럼 표현합니다.

만약 우리가 the impulse train's frequency domain (e and f) 에서 0.02 보다 높은 모든 주파수 영역을 잘라내면, 우리는 마침내 원본 신호와 같은 주파수 그림 (i)를 마주하게 됩니다. 이제 푸리에 변환을 반대로 적용하면, 원본 신호 (g)를 다시 얻습니다. 이 과정을 복원(Reconstruction)이라 부릅니다.

만약 이것이 실제 시스템이라면, 우리는 샘플한 값의 유한 세트를 숫자화 할 수도 있으며, 그것을 트랜스미션나 스토리지 혹은 어떤 다른 디지털 어플리케이션에 사용할 수 있습니다. 우리는 수신단말 혹은 저장된 신호를 다시 재생하는데에서 신호를 복원 할 것입니다. 실제로는 우리는 복원을 수행하기 위해 주파수 도메인을 잘라버리는 대신에 시간 도메인의 low-pass 필더를 적용할 수도 있습니다.
Aliasing due to improper sampling
Impulse train frequency 그림 (e)에서 원본 주파수 그림 (b)가 어떻게 반복되어졌는지 관측하세요. 당신이 샘플링 주파수를 증가시킬때, Impulse train의 밀도는 확실하게 증가합니다, 그러나 주파수 도메인에서 반복되어지는 섹션은 서로서로 더 멀어집니다. 거꾸로, 당신이 샘플링 주파수를 감소시키면, 반복되어지는 섹션들은 그들이 서로 더해지며 겹쳐지기 시작할때까지 서로서로 가까워집니다. 이렇게 서로 겹쳐지기 시작하는 주파수를 Nyquist rate라고 부릅니다.
원본 주파수 그림 (c)에서, 우리는 [0.0, 0.02] 범위에서 0이 아닌 값을 갖고 있으며 두개의 ▲s 로 표시합니다. 이 범위는 원본 신호의 대역폭이라고 불려집니다(앞서 말한 음의 주파수들에서의 대칭 때문에 우리가 양의 주파수 [0.0, 0.5]만 살표보고 있다는 것을 기억하세요).
Nyquist rate 는 2배의 대역폭입니다. 적절하게 우리의 신호를 샘플하기 위해서 우리는 적어도 0.02 X 2 = 0.04 Hz 나 그 이상이 필요하다는 의미 입니다.
만약 우리가 이 빈도 이하로 샘플링 하는 경우 어떤일이 발생하는지 봅시다. 그림 (j) 부터 (o)는 위의 내용과 유사한 처리를 하지만 샘플링을 적은 빈도로 합니다.

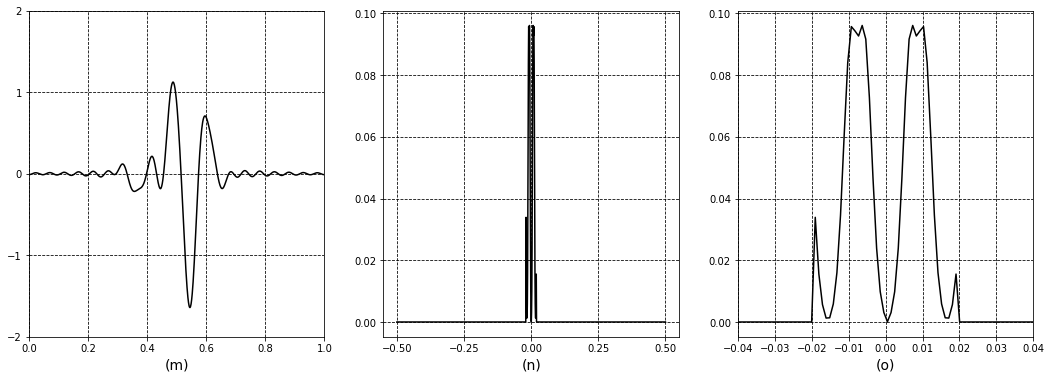
우리가 깔끔하고 반복된 주파수 그림(i)를 얻지 못하는 것에 주목해주세요. 결과적으로, low-pass-filtered 주파수 그림(o)는 깔끔하지 않습니다, 그리고 복원되어진 신호 (m)은 원본 신호(a)와 같지 않습니다.
이것을 앨리어싱이라고 부릅니다, 원본 신호의 더 높은 주파수들이 복원되어진 신호에서의 낮은 주파수로 가장하기 때문입니다.
샘플링과 복원에서 발생한 놀라운 사실은 만약 연속된 시간의 신호가 적절히 샘플링 되어지면, 유한한 샘플 세트의 결과는 원본 신호의 무한한 샘플들의 정보의 양과 같습니다!
Aliasing in computer graphics
지금까지, 우리는 정식으로 설명한 디지털 신호 처리 이론에서 앨리어싱을 살펴봤습니다.
오디오 처리와 그래픽스의 결정적인 차이는, 오디오 시스템에서는, 우리는 이산-시간 신호를 연속적인 시간 신호를 생성하기 위해서 복원합니다. 글고 그것이 최종 출력물이다(즉, 스피커의 막으로 만들어진 진동들). 그러나 그래픽스에서는, 우리의 최종 결과물이 이산입니다-(즉, 필셀 값들).
그럼에도, 만약 우리가 Nyquist rate 보다 낮게 샘플하면, 앨리어싱은 여전히 발생합니다. 다른 말로하면, 알리어싱은 복원 중이 아니라 샘플링 도중 발생합니다.
이제 우리는 실전에서 앨리어싱을 현상의 세가지 다른 방식을 살펴볼 것입니다:
Rasterization aliasing
이것은 가장 널리 알려진 앨리어싱 현상은-삼각형 메시를 따라 발생하은 jagged edges 입니다. 이것이 발생하는 이유를 이해하기 위해서, 검은 배경위에 1D로 슬라이스 된 하얀색 삼각형을 봅시다. 삼각형이 없는 곳은, 기반 연속 함수의 값이 0 입니다. 삼각형이 시작되면 그 값은 즉시 1로 점프 합니다. 이 말은 기반 연속 함수가 Step function 이라는 것입니다.
당신이 이 삼각형 슬라이스를 스크린에 레스터라즈 할때, 당신은 기본적으로 기반 함수 픽셀의 가운데를 샘플링하고 있습니다.
기반 함수는 step 이기 때문에, 대역폭은 무한대 입니다(급작스럽게 변화하기 때문). 유한한 양의 해상도는 앨리어싱을 완전히 피하기 충분하지 않다는 의미입니다.
좌측 그림은 기반 Step function을 표현합니다, 그리고 바닥의 strip은 16 픽셀의 중심이 샘플 되었을 때, 어떻게 그것이 보여질 것인지를 보여줍니다. 우리가 삼각형을 움직일때, 픽셀이 어떻게 점프하는지 알 수 있습니다, 비록 기반 함수가 부드럽게 이동할지라도 그렇습니다. 이것이 정확히 2D에서 jagged edges를 발생시키는 것입니다.
오른쪽 그림은 (픽셀) 샘플링 주파수의 절반 cut-off 주파수로 step function의 low-pass-filtered 버젼을 보여줍니다. 이 픽셀 strip은 여기서 그레이스케일 값을 사용하여 부드러운 움직임을 보여줍니다. 알아야할 중요한 것은 이 안티알리어싱 필터는 흐리지 않다는 것입니다. 흐림은 샘플링 뒤에 발생했지만 이것은 이전에 적용되어졌습니다.
실제로는, 레스터라이져들은 기반 함수들에 분석적인 필터들을 적용하지 않습니다. 대신에, 실제 안티앨리어싱 기술은 픽셀 중심 주변 이웃을 supersample 합니다, 그리고 가중합을 수행합니다. 이 가중합은 저렴한 low-pass 필터로 보일 수 있습니다. 즉, 만약 당신이 이웃 픽셀의 평균을 구한다면, 상자필터가 수행됩니다. 만약 거리-가중합을 한다면, 가우시안 필터와 비슷한 것이 수행됩니다. supersample 된 이미지를 위해서 필터를 선택할 때, 당신은 퍼포먼스와 주파수 cutoff의 균형 맞추도록 해야합니다.
Supersampling 중에, 앨리어싱은 기술적으로 여전히 발생합니다, 그러나 당신은 더 많은 사용가능한 대역폭을 얻습니다, 그래서 jagged edges가 덜 눈에 띕니다.
삼각형의 서브픽셀이 희미해졌다 말았다 하는 것은 역시 같은 문제의 또 다른 현상입니다.
마지막으로, 레스터라이제이션을 바라보는 다른 방법이 있습니다-몇몇 문서의 제목(A pixel is not a little square [PDF])들과는 다르게, 하나의 픽셀은 작은 사각형 하나로 보여집니다. 이 관점에서, 당신은 픽셀영역에 레스터라이즈 되어지고 있는 프리미티브의 영역을 계산하기 위해, 기반 함수를 통합하길 원할 것입니다. 폰트와 SVG 레스터라이제이션은 이 각도로 부터 문제에 접근 할 수 있습니다; 3D 그래픽스은 보통 그렇지 않습니다.
Texture aliasing
Nyquist rate는 신호에 포함되어있는 정보의 측정으로 보여질 수 있습니다. 만약 신호하나가 대역폭 f/2 를 가지고 있다면, 주파수는 정보를 보존하기 위해서 f보다 더 높게 샘플 되어져야만 합니다. 거꾸로, 만약 이산 신호가 f 주파수로 샘플 되어졌다면, f/2 보가 거 적은 대역폭 정보를 가져야 합니다.


첫 원본 이미지는 fo 주파수로 샘플링 되어졌다고 합시다. 그리고나서 그것은 fm 에 낮은 샘플링 주파수로 샘플링 되면서 minified 되어집니다(역주 : 하나의 픽셀에 여러개의 픽셀이 대응되는 경우를 말함, 반대는 magnified 로 한개의 픽셀이 여러 픽셀로 들어가면서 깍두기 모양을 만듬). 만약 원본 이미지가 밴드에서 주파수 [fm/2, fo/2]를 포함 한다면, 그들은 앨리어스 될것 입니다. 당신은 두번째 이미지에서 Moiré patterns 형태를 볼 수 있습니다.

이것은 원본 주파수 보다 더 낮은 주파수로 샘플링 한 경우, 그래픽스의 임의의 점에서 발생합니다, 아래와 같은:
- 더 먼곳에서 보기 때문에 텍스쳐가 minified 되는 경우. 밉맵핑은 low-pass pre-filtering 텍스쳐와 더 낮은 해상도의 복사본을 저장하여서 이 문제를 고칩니다. minified 된 텍스쳐를 바라볼때, GPU는 더 가까운 큰 밉맵을 선택합니다, 그래서 앨리어싱 된 대역폭이 최소화 됩니다.
- 텍스쳐가 원근 왜곡 되어있는 경우. 이것은 지면 텍스쳐에서 가장 자주 발생합니다, 그래서 이전 문제와 관련되어있습니다. 여기에, 카메라와 더 가까운 텍스쳐의 부분들은 더 높은 빈도로 샘플링 되어집니다, 반면에 거리가 있는 것들은 덜빈번하게 샘플링 됩니다. GPU는 anisotropic 필터링으로 이것을 고칩니다. 즉, 로컬 샘플링 빈도에 따라서 같은 지오메트리에 다른 밉맵을 사용합니다.
Shading function aliasing
이것은 텍스쳐 앨리어싱과 가깝게 관련되어 있습니다만, 고치기에는 더 복잡할 수 있습니다. 각각의 픽셀은 기반 함수에 따라 쉐이딩 되어집니다. 이 함수는 복잡해지며 픽셀 위치, 지오메트리컬 노말, 텍스쳐 노말, 디퓨즈 컬러, 러프니스, 라이트 위치, 등등 의 파라메터를 가집니다. 그리고 컬러를 출력으로 생산해냅니다. 만약 이 함수의 출력의 Nyquist rate 가 우리의 픽셀 주파수 보다 더 크다면, 앨리어싱은 발생할 것입니다.
이것이 그래픽스에서 앨리어싱을 살펴보는 가장 일반화된 방법입니다, 그리고 두새의 위의 변형도 이 카테고리에 맞출 수 있습니다. 나는 specular aliasing 같은 문제가 이 추상화 레벨에서 설명되어질 수 있기 때문에 그것을 분리하여 언급했습니다.
TL;DR
임의의 band-limited 연속 신호는 Nyquist rate 로 불리는 주파수를 가집니다. 앨리어싱을 피하기 위해서, 당신은 그 rate 보다 더 높게 샘플링 해야 합니다. 대안으로, 당신은 당신의 샘플링 예산보다 더 높은 신호는 주파수를 제거 할 수 있습니다.
결론적으로, 나는 이 글이 앨리어싱의 토대가 되는 것들이고 그것의 추적하는 발법에 대해서 당신에게 더 나은 아이디어를 주길 바랍니다. 그래픽스의 수 많은 영역이 이 주제를 다룹니가, 그래서 이것은 이해하기 쉽습니다. 나는 파이썬 코드를 실행해보기를 권장합니다. 그것은 여기에서 공용 도메인으로 무료로 사용가능 합니다
'Graphics > 참고자료' 카테고리의 다른 글
| [번역]Convolution (0) | 2020.05.13 |
|---|---|
| [번역] Tiled Forward Shading (0) | 2020.05.09 |
| [번역]Light Indexed Deferred Lighting (0) | 2020.03.23 |
| [번역]Radiometry (Steve Marschner, Cornell University) (0) | 2020.02.29 |
| [번역]Dual paraboloid shadow mapping (2) | 2020.02.15 |




