| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- unrealengine
- vulkan
- scattering
- Nanite
- texture
- DX12
- RayTracing
- SIMD
- UE5
- Wavefront
- GPU
- Shadow
- 번역
- wave
- hzb
- VGPR
- optimization
- shader
- Study
- DirectX12
- forward
- Graphics
- scalar
- atmospheric
- SGPR
- GPU Driven Rendering
- rendering
- ShadowMap
- ue4
- deferred
- Today
- Total
RenderLog
[번역]Convolution 본문
개인 공부용으로 번역한 거라 잘못 번역된 내용이 있을 수 있습니다.
또한 원작자의 동의 없이 올려서 언제든 글이 내려갈 수 있습니다.
출처 : https://homepages.inf.ed.ac.uk/rbf/HIPR2/convolve.htm
Convolution
Convolution은 간단한 수학적 연산이다. 이것은 많은 흔한 이미지 처리 연산의 기반입니다. Convolution은 2개의 숫자 배열의 'Multiplying together' 방식을 제공합니다, 보통은 서로 다른 사이즈, 같은 차원일 수도있음, 이것으로 세번째의 같은 차원의 숫자 배열을 생산합니다. 이것은 출력 픽셀의 값이 입력 픽셀의 간단한 선형 조합이 되도록 구현는 것은 이미지 처리에 사용되어질 수 있습니다.
이미지 처리의 문맥에서, 입력 배열 중 하나는 보통 Graylevel(역주 : grayscale 이미지, 회색 이미지) 이미지 입니다. 두번째 배열은 보통 훨씬 작습니다. 그리고 역시 2차원(픽셀 하개의 크기이라 할지라도), 그리고 커널이라고 알려져있습니다. 그림 1은 이미지와 Convolution을 사용하기 위해서 사용하는 커널 예제를 보여줍니다.

Convolution은 image에 커널을 이미지의 경계범위내에서 커널이 잘맞는 모든 위치에, 보통은 좌상단에서 시작, 들어오도록 이동시키며 수행됩니다. (아래에서 설명한것 처럼, 이미지의 가장자리에 무엇을 할지에 따라서 구현은 달라진다는 것을 주의해야함). 각 커널의 위치는 한개의 픽셀 출력에 대응됩니다, 그 출력은 커널값과 기반이미지 픽셀 값을 커널내의 각각의 cell에 대하여 서로 곱하여서 계산되어집니다, 그리고나서 모든 숫자를 서로 더해줍니다.
그래서, 우리의 예제에서는, 출력 픽셀의 우하단 픽셀 값이 아래와 같이 주어질 것입니다:

만약 이미지가 M 행 그리고 N 열 이고, 커널은 m 행과 n 열을 가지고 있다면, 출력 이미지 크기는 M - m + 1 행 그리고 N - n + 1 열 입니다.
수학적으로 우리는 다음과 같이 convolution을 쓸 수 있습니다:
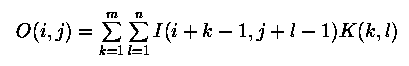
i는 i 부터 M - m + 1 그리고 j는 1 부터 N - n + 1 입니다.
알아둬야 할 점은 많은 Convolution이 이것보다 더 큰 출력 이미지를 만드는 것입니다. 왜냐하면 커널이 이미지 범위내에 딱 맞는 제약사항을 완화하기 때문입니다. 대신에, 커널의 좌상단만 이미지 범위내에 두고 이미지의 모든 위치로 커널을 이동시키는 것으로 보통 구현합니다. 그러므로 커널의 우하단은 이미지와 겹칩니다. 이 접근의 장점은 출력 이미지가 입력 이미지와 같은 것입니다. 불행히도, 이미지의 우하단 값을 계산하기 위해서, 이미지의 끝 바깥 쪽에 있는 커널의 확장 부분에 위치하는 픽셀 입력 값을 어떻게 할지 고민하는 것이 필요합니다. 보통 이미지의 바깥쪽 값은 0 값이 선택되어집니다, 그러나 이것은 종종 그 위치에서 이미지의 출력을 왜곡시킬 수 있습니다. 그러므로 보통 만약 convolution 이러한 구현을 사용하고 있다면, 비정상적인 영역을 제거하기 위해서 이미지를 자르는 것이 낫습니다. 오른쪽에서 n - 1 픽셀 그리고 아래쪽에서 m - 1 픽셀을 제거하는 것이 이 부분을 정리해 줄 것입니다.
Convolution은 여러가지 연산을 특히 공간 필터와 특징 탐지를 구현하기 위해서 사용되어질 수 있습니다.
예를들어 Gaussian smoothing 과 Sobel edge detector 가 있습니다.
©2003 R. Fisher, S. Perkins, A. Walker and E. Wolfart.
'Graphics > 참고자료' 카테고리의 다른 글
| [번역][Nvidia White Paper] Volume Light (0) | 2020.05.28 |
|---|---|
| [번역] Forward+ : A Step Toward Film-Style Shading in Real Time (0) | 2020.05.17 |
| [번역] Tiled Forward Shading (0) | 2020.05.09 |
| [번역]Aliasing in computer graphics (0) | 2020.04.10 |
| [번역]Light Indexed Deferred Lighting (0) | 2020.03.23 |




