| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- deferred
- Shadow
- GPU
- UE5
- shader
- vulkan
- unrealengine
- GPU Driven Rendering
- SGPR
- RayTracing
- scalar
- Nanite
- SIMD
- optimization
- ue4
- Graphics
- DirectX12
- DX12
- hzb
- Wavefront
- 번역
- texture
- VGPR
- Study
- ShadowMap
- forward
- scattering
- rendering
- wave
- atmospheric
- Today
- Total
RenderLog
[번역]Gaussian Smoothing 본문
개인 공부용으로 번역한 거라 잘못 번역된 내용이 있을 수 있습니다.
또한 원작자의 동의 없이 올려서 언제든 글이 내려갈 수 있습니다.
출처 : https://homepages.inf.ed.ac.uk/rbf/HIPR2/gsmooth.htm
Gaussian Smoothing

간단한 설명
가우시안 스무딩 연산은 이미지 블러와 디테일과 노이즈 제거에 사용되는 2D Convolution 연산입니다. 이런 의미에서 평균필터와 비슷한 의미입니다, 그러나 그것은 가우시안의 모양이 혹(종 모양)으로 표현되는 다른 커널을 사용합니다. 이 커널은 아래에 자세하게 소개되는 특별한 몇몇 속성이 있습니다.
작동 방식
1D 가우시안 분포는 형태를 가지고 있습니다:

분산의 표준편차에서. 우리는 역시 분포 0의 평균을 가지고 있다고 가정합니다.
(즉, line x = 0 에서 중심이 맞춰져있습니다.) 그 분포는 그림1에서 보여줍니다.

2D에서는, 등방성(isotropic) (즉, 원형으로 대칭인) 가우시안 형태를 가집니다:
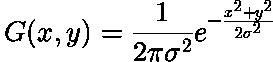
이 분포는 그림2에서 보여집니다.
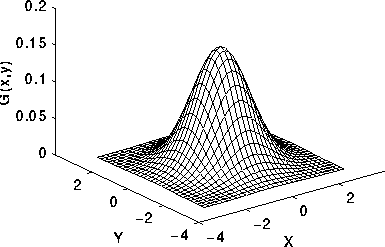
가우시안 스무딩의 아이디어는 2D 분포를 점확산(point-spread) 함수로 사용하는 것입니다, 그리고 이것은 convolution으로 이루어집니다. 이미지는 개별의 픽셀의 모음으로 저장되어지므로 우리는 우리가 convolution을 수행하기 전에 가우시안 함수에 대해서 개개별로 근사를 생성해야 합니다. 이론에서, 가우시안 분포는 모든 곳에서 0이 아닙니다, 그것은 무한하게 큰 convolution 커널을 요구할 것입니다, 그러나 실제로는 대략 평균으로 부터 3개의 표준편차 보다 더 큰것은 0으로 합니다. (it is effectively zero more than about three standard deviations from the mean), 그리고 우리는 이 점에서 커널 잘라낼 수 있습니다. 그림3은 적절한 정수값으로 된 a가 1.0에서의 가우시안 근사의 convolution 커널을 보여줍니다. 가우시안을 근사하기 위해서 어떻게 mask의 값을 선택하는지는 확실하지 않습니다. Mask 픽셀의 가운데에서 가우시안의 값을 사용할 수 있습니다, 그러나 이것은 정확하지 않습니다. 왜냐하면 가우시안 값은 픽셀에서 비선형으로 변하기 때문입니다. 우리는 전체 픽셀에 가우시안의 값을 통합할 수 있습니다.(0.001 을 가우시안에 더해주므로써). 전체 합은 정수값이 아닙니다: 우리는 코너 값이 1을 갖도록 배열을 재조정합니다. 끝으로, 273이 Mask의 모든 값의 합입니다.
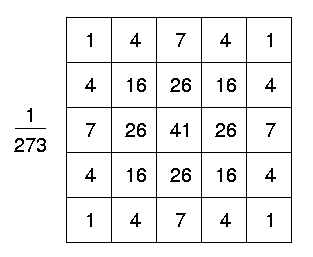
적절한 커널이 계산되어지면, 가우시안 스무딩은 표준 Convolution 방식을 통해 수행되어질 수 있습니다. Convolution은 실제로 꽤 빠르게 수행되어집니다. 위에 보여진 2D 등방성 가우시안 방정식은 x와 y 컴포넌트로 분리되어질 수 있기 때문입니다. 그래서 2D Convolution은 x방향의 1D 가우시안으로 첫 Convolving 그리고나서 또다른 1D 가우시안을 y 방향으로 Convolving 할 수 있습니다. (가우시안은 실제로 이런 형태로 분해 될 수 있는 완전히 원형으로 대칭되는 연산입니다.) 그림4는 1D의 x 컴포넌트 커널을 보여줍니다. 이 커널은 그림3의 전체 커널을 생성하기 위해서 사용됩니다.(273으로 재조정 한 후에, 경계 주위 픽셀의 한 열(Row)를 반올림과 잘라냄 왜냐하면 그 값들은 거의 0에 가까운 값이기 때문. 이것은 위에서 보여준 것 처럼 7x7 매트릭스를 5x5 로 줄여준다) y 컴포넌트는 완전히 동일하지만 방향이 세로입니다.

넓은 표준편의 가우시안 스무딩을 계산하기 위한 다른 방법은 작은 가우시안으로 여러번 처리하여 통합하는 것입니다. 계산이 복잡하지만 처리가 하드웨어 파이프라인에서 수행되어진다면, 적용할 수 있습니다.
가우시안 필터 엔지니어링 어플리케이션에만 유용한게 아니라 전산생물학자의 관심또한 끌고 있습니다. 왜냐하면 그것은 어느정도 생물학적으로 타당한 속성을 가지고 있기 때문입니다. 즉. 뇌의 시각경로에 있는 몇몇 세포는 근사된 가우시안 반응을 가집니다.
사용을 위한 가이드라인
가우시안 스무딩의 효과는 평균 필터와 하 비슷한 방식으로 이미지를 블러하는 것입니다. 스무딩의 정도는 가우시안의 표준 편차에 의해서 결정되어집니다. (넓은 표준편차의 가우시안은, 물론, 넓은 Convolution 커널이 정확한 표현을 위해서 요구됩니다.)
가우시안의 결과는 인접한 각 픽셀의 가중 평균(weighted average) 입니다, 평균은 중간값의 픽셀에 더 가중됩니다. 이것은 평균 필터가 균일하게 가중평균되는 것과 대조적입니다. 이것 때문에, 같은 필터의 평균 필터보다 가우시안은 더 부드럽고, 에지가 더 잘 보존됩니다.
스무딩 필터로 가우시안을 사용하는 한가지 이유는 그것의 주파수 응답(frequency response) 때문입니다. 대부분의 Convolution 기반 스무딩 필터는 저역 통과 주파수 필터(lowpass frequency filters)처럼 행동합니다. 이 효과는 높은 공간의 주파수 부분을 이미지에서 제거한다는 의미입니다. Convolution 필터의 주파수 응답, 즉. 다른 공간 주파수의 그것의 효과, 필터의 푸리에 변환을 하므로써 보여질 수 있습니다. 그림5는 너비 5의 1D 평균 필터의 주파수 응답과 = 3의 가우시안 필터를 보여줍니다.
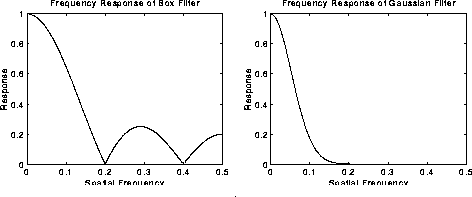
두 필터 모두 저 주파수들 보다 고 주파수를 감쇄시킵니다, 그러나 평균 필터는 그것의 주파수 응답에서 진동을 나타냅니다. 반면에 가우시안은 진동을 보여주지 않습니다. 실제로, 주파수 응답 곡선의 모양은 그것 자체가 (절반) 가우시안 입니다. 그래서 적절한 크기의 가우시안 필터를 선택하므로써 우리는 필터링(이경우 평균 필터가 아님) 후의 이미지에서 어떤 범위의 공간 주파수들이 여전히 남아있을 것인지 확신할 수 있습니다. 이것은 Zero Crossing 섹션에서 언급한것 처럼 몇몇의 에지 검출 기술에 영향을 주었습니다. (가우시안 필터는 Canny 에지 검출 유도에 사용된 기준에 따라 에지 검출을 위한 최적화된 스무딩 필터와 유사한 것으로 밝혀졌습니다.)
우리는 점점 더 큰 스무딩 효과를 보여주기 위해서 가우시안 필터를 사용했습니다.

이 이미지는

가우시안 = 1.0 (그리고 커널 사이즈 5x5)의 효과를 보여줍니다.
이 이미지는

가우시안 = 2.0 (그리고 커널 사이즈 9x9)의 효과를 보여줍니다.
이 이미지는

가우시안 = 4.0 (그리고 커널 사이즈 15x15)의 효과를 보여줍니다.
우리는 이제 가우시안 필터를 노이즈 감소에 고려중입니다. 예를들어, 어떤 이미지가

평균 0과 σ = 8의 가우시안 노이즈에 의해 손상되었다고 합시다.
5x5로 가우시안으로 스무딩을

수행합니다. (평균필터와 중앙값 필터로 부터 얻어진 결과를 비교)
Salt and Pepper 노이즈는 가우시안 필터에 더 까다롭습니다.
여기 우리는 1%의 Salt and Pepper 손상을 가진 이미지를 스무딩 할 것입니다. (즉, 개개별 비트는 아마 1% 정도 확률로 뒤집혀졌음).
이 이미지는

가우시안 스무딩을 보여줍니다. (위와 같은 Convolution 사용).
원본과

비교하면 여전히 많은 노이즈가 존재합니다, 비록이 크기가 다소 감소했지만, 넓은 공간 영역으로 퍼졌습니다. 표준편차를 증가시키면, 노이즈의 강도가 계속 감소 혹은 흐려지게 됩니다, 뿐만아니라 높은 주파수의 디테일 (즉, 에지)가 크게 감쇄됩니다, 보는것과 같이

이런 종류의 노이즈는 중앙값 필터로 감소시키는 것이 더 낫습니다, Conservative smoothing or Crimmins Speckle Removal.
인터렉티브 실험
당신은 여기를 클릭하므로써 인터렉티브한 실험을 할 수 있습니다.
연습
1. 가우시안 노이즈 (평균 0, σ = 13)로 부터 손상된 이미지로 부터

시작해서 평균 필터와 가우시안 필터로 다양한 크기로 계산합니다, 그리고 각각을 노이즈 제거 vs 디테일 잃음 측면에서 비교합니다.
2. 평균으로 부터 얼마나 많은 표준편차가 가우시안 최대값의 5% 수준으로 떨어지는가? 이것의 기반은 적절한 사각형 커널 크기를 가우시안 필터 너비 = s 로 제안합니다.
3. 이미지를 가우시안 필터로 가우시안 스무딩 하므로써 주파수 반응을 추정하세요, 그리고 전과 후의 푸리에 변환을 수행하세요. 평균 필터의 주파수 반응과 이것을 비교하세요.
4. 같은 커널 사이즈의 가우시안 필터가 평균 필터에 비해 얼마나 많은 시간을 사용하나요? 두 경우에서 주목할 점은 Convolution은 커널의 특징을 활용하므로써 상당한 속도 증가를 얻을 수 있는 것입니다.
참고자료
E. Davies Machine Vision: Theory, Algorithms and Practicalities, Academic Press, 1990, pp 42 - 44.
R. Gonzalez and R. Woods Digital Image Processing, Addison-Wesley Publishing Company, 1992, p 191.
R. Haralick and L. Shapiro Computer and Robot Vision, Addison-Wesley Publishing Company, 1992, Vol. 1, Chap. 7.
B. Horn Robot Vision, MIT Press, 1986, Chap. 8.
D. Vernon Machine Vision, Prentice-Hall, 1991, pp 59 - 61, 214.
Local Information
이 연산에 대한 특정 정보는 여기서 찾을 수 있을 것입니다.
더 일반적인 local HIPR 설치에 대한 도움은 Local Information 입문 섹션에서 가능합니다.
©2003 R. Fisher, S. Perkins, A. Walker and E. Wolfart.
'Graphics > 참고자료' 카테고리의 다른 글
| [번역]Life of a triangle - NVIDIA's logical pipeline (0) | 2020.06.21 |
|---|---|
| [번역][UE4]Rendering Wounds on Characters in UE4 (0) | 2020.06.12 |
| [번역][Nvidia White Paper] Volume Light (0) | 2020.05.28 |
| [번역] Forward+ : A Step Toward Film-Style Shading in Real Time (0) | 2020.05.17 |
| [번역]Convolution (0) | 2020.05.13 |




