Color Science

Color Science

 

최초 작성 : 2021-12-25

마지막 수정 : 2022-01-01

최재호

 

XYZ <-> sRGB color space 의 설명을 xyY <-> sRGB 로 잘못 설명한 부분 수정 - updated 2022-01-01

 

목차

1. 목표

2. Visible spectrum
  2.1. Spectral power distribution (SPD)
3. The anatomy of human vision
  3.1. Cells
  3.2. LMS, V function
    3.2.1. Radiant flux
    3.2.2. Luminous flux
  3.3. Tristimulus values and primaries
4. The CIE RGB color space
  4.1. color matching experiments
  4.2. Negative Primaries
5. The CIE XYZ color space
  5.1. CIE RGB color space 에서 CIE XYZ color space 로 변환
  5.2. Normalized chromaticity coordinates xyz
  5.3. xyY color space
  5.4. The CIE xy chromaticity diagram
  5.5. illuminant D65 흰색의 정의
6. The sRGB color space
  6.1. sRGB color space 의 Primaries
    6.1.1. sRGB Primaries의 Luminance Y 구하기
  6.2. XYZ color space 를 sRGB color space로 변환
  6.3. sRGB color space를 XYZ color space로 변환 그리고 sRGB 컬러로 부터 luminance 얻기
7. 실제 연산 테스트
  7.1. CIE XYZ color matching function 그려보기

  7.2. CIE XYZ color matching function으로 CIE_RGB color matching function 생성하고 그려보기

  7.3. sRGB Primaries의 luminance 구하기

  7.4. sRGB 에서 XYZ color space 변환 매트릭스 구성
  7.5. XYZ 에서 sRGB color space 변환 매트릭스 구성

  7.6. XYZ 에서 sRGB color space 변환 매트릭스 테스트
8. References

 

 

1. 목표

Foundations of Game Engine Develpment 2 의 Color Science 파트를 읽어보고 이해한 내용을 실제 테스트 해봅시다.

 

2. Visible spectrum

빛은 다양한 파장(wavelength)의 범위를 가지고 있습니다. 인간이 감지할 수 있는 전자기방사선(electromagnetic radiation)의 파장은 대략 380 nm ~ 780 nm 입니다. 이 글에서는 각각의 파장을 1nm 단위로 분리하여 에너지를 측정합니다.

그림1. Visible spectrum (출처 : 레퍼런스2)

2.1. Spectral power distribution (SPD)

라이트 소스에서 직접 나오는 광원이나 표면에 반사되어서 나오는 라이트는 많은 서로 다른 파장을 가집니다. 이런 파장별 에너지 조합을 라이트의 SPD라 부릅니다.

• 이러한 파장들의 분포는 P(λ) 함수로 표현할 수 있습니다.
• P(λ) 는 각 파장 λ 에 대응하는 power를 반환합니다.

3. The anatomy of human vision

3.1. Cells

우리 눈은 빛을 감지하기 위해서 2종류의 세포

• Cone cells
  • 눈의 중앙 근처에 3 종류가 있고 색상을 감지함
    • L(Red) : 63% 분포
    • M(Green) : 31% 분포
    • S(Blue) : 6% 분포
  • Phtopic vision 이라 부름
• Rod cells
  • 어두운 빛 조건에서 강해짐
  • 색을 구분하는 능력은 없음
  • Scotopic vision 이라 부름

3.2. LMS, V function

L, M, S 세포들의 상대적인 민감도를 표현이 아래 그림2에 있습니다. 그리고 각각을 L, M, S Curve 로 나타냅니다. (또는 function 이라고도 부름)

LMS 이외에 밝기에 대한 Curve가 추가되어있습니다. 바로 Luminosity function V(λ) 있으며 아래와 같은 특성이 있습니다.

• 3개의 서로 다른 cone cell의 합으로 근사 가능
• 555nm (green-yellow)에서 luminosity function이 가장 높음. 인간이 가장 밝게 느끼는 색상 부분임.
• blues, violets, deep red는 꼬리 끝 부분에 있기 때문에 더 어두운 색상으로 느껴짐

그림2. L, M, S, V functions (출처 : 레퍼런스1)

3.2.1. Radiant flux

그림3. Radiant flux (출처 : 레퍼런스1)

라이트 소스로 부터 나오는 power의 총양을 radiant flux를 ΦE 라고 부릅니다.

• 전체 wavelengths에 있는 power를 모두 합산한 값입니다.
• Radiant flux는 watt 단위로 측정되며, P(λ) 함수는 보통 W/nm(watt per nanometer) 단위를 사용합니다.
• ΦE 에서 E는 energetic, 즉 radiant flux는 순수하게 라이트 소스로 부터 방출되는 에너지를 기반함

 

3.2.2. Luminous flux

 

그림4. Luminous flux (출처 : 레퍼런스1)

 

SPD인 P(λ)와 luminosity function V(λ)를 모두 고려하는 측정양입니다.

• 단위는 lumens (lm)
• ΦV의 V는 visual, luminous flux는 wavelength에 대한 인간의 시각적 민감도를 포함함.
• 555nm에서 683 lumen per watt 로 가장 높은 값을 가짐. (이 지점이 luminosity funtion이 가장 높은 지점)
• 683 값을 곱하여 주는 이유는 luminous flux 값이 양초와 같이 역사적으로 사용하던 단위와 비슷하게 하기 위함.

 

3.3. Tristimulus values and primaries

많은 라이트의 파장들이 있지만 결국 3종류의 cone cell 이 각각의 신호를 만들어서 뇌로 보내고 뇌가 그 신호를 처리합니다. 신호의 크기는 각 파장의 라이트 강도의 가중합(weighted sum)입니다. 가중치(weights)는 그림2의 sensitivity curves 입니다. 신호는 SPD와 cone sensitivity function 의 곱을 적분 한 것 나누기 전체 wavelength의 범위 입니다.

 

같은 세개의 신호 크기를 SPD의 적분으로 만드는 방법히 무한히 많습니다. 그래서 SPD가 전혀 같지 않더라도 동일한 색상을 만들어낼 수 있습니다. 이렇게 일치하는 구성을 metamers 라고 합니다. 이 metamers는 L, M, S cone이 동일한 크기로 각각 자극 하기 때문에 인지하는 색상은 모두 동일합니다. 이렇게 특정 색상과 동일하게 인지하기 위해서 세가지 색상을 섞을 수 있는데 이때 각 색상의 양을 나타내는 값을 Tristimulus values라고 합니다.

 

색상은 다른 3가지 색상의 혼합으로 나타낼 수도 있습니다. 2개의 라이트를 혼합할 때, 분리된 L, M, S Trisimulus value는 거의 정확히 선형적으로 더해집니다.

Tristimulus values가 선형적으로 더해질 수 있다는 것은 이 값들이 3차원 벡터를 이룬다는 의미입니다. 그러나 이 벡터 공간은 기저 벡터가 물리적으로 가능한 Tristimulus value와 일치하지 않기 때문에 조금 특이합니다. 왜냐하면 오직 한개의 cone cell만 자극하는 라이트의 파장는 없고, 2개나 3개가 같이 자극을 받기 때문입니다.

 

물리적으로 의미있게 하기위해서 3개의 개별 파장 세트를 선택합니다. 이것을 primaries라고 부릅니다. 이 primaries를 조합하여 인지 가능한 넓은 범위의 색상을 생성할 수 있습니다.

이렇게 정해진 Primaries 통해 1920s color matching experiments 를 수행합니다. 여기서 Red, Green Blue 라이트를 LMS cone 자극의 기조로 정합니다.

선택된 Primaries의 파장

• red : 700 nm
  • L cone은 넓은 범위의 sensitivity고 대부분의 가장 붉은을 잘 인지 할 수 있기 때문에 선택됨. 그러나 yellow part 의 스펙트럼에서 L 의 자극이 가장 큼
• green : 546.1 nm
• blue : 435.8 nm
  • green과 blue는 수은등에서 쉽게 만들 수 있고, green, blue에서 M과 S의 peak sensitivities여서 선택됨

 

4. The CIE RGB color space

4.1. color matching experiments

1920s color matching experiments 는 아래와 같이 수행됩니다. 단일 파장에서 나오는 색상과 나머지 Primaries를 조합한 값과 비교하여 일치하는 값을 찾아냅니다.

그림5. 1920s Color matching experiments (출처 : 레퍼런스3)

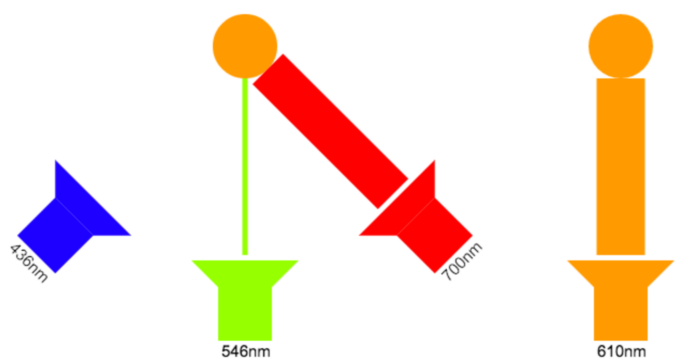
각각의 파장이 내는 색을 만들기 위해서 필요한 Primaries의 양을 모두 실험합니다. 그리고 아래 그림 처럼 CIE RGB color matching function (CIE RGB color matching curve)를 만들어냅니다. 아래 그림을 보면 마이너스 값을 가지는 구간이 있는데, 자극이 마이너스가 될 수는 없으므로 말이 안됩니다. 이러한 구간은 Primaries의 조합으로 생성할 수 없는 라이트라 조금 다른 방법을 사용하였습니다. 계속해서 어떻게 이 부분을 처리했는지 알아봅시다.

그림6. CIE RGB color matching function (출처 : 레퍼런스1)

4.2. Negative Primaries

마이너스가 나오는 부분은 Reference Light(Primaries 조합으로 만들고자하는 단일 파장)에 Primaries 값을 추가하여 Reference Light와 Primaries Light를 맞춰줍니다. 이러한 트릭을 사용하여 Primaries 로 컬러 매칭이 불가능한 Spectrum들도 모두 정량화 할 수 있었습니다. 이런 점은 Tristimulus value가 정확히 선형적으로 더해질 수 있기 때문에 가능한 것 같습니다. 실제 물리적으로는 음수로 나타낼 수 없지만 수치상으로 Tristimulus value를 선형적으로 연산하는 것은 충분히 가능할 것입니다.

그림7. Color matching experiments 중 생성할 수 없었던 monochromatic light(단일 파장에서 나오는 빛으로 만들어진 단색광, 즉 특정 파장 1개의 색상) 를 negative primaries 트릭으로 해결함 (출처 : 레퍼런스3)

 

실험의 결과로 나온 r(λ), g(λ), b(λ) 컬러 매칭 함수를 얻었습니다. 이 함수로 부터 알 수 있는 점은 아래와 같습니다.

• 이 함수들은 주어진 λ에 해당하는 단색광(monochromatic light) 에 red, green, blue primaries가 얼마나 필요한지를 보여줌.
• 이 함수는 1931 International Commission on Illumination (CIE, 프랑스 이름의 약자를 땀)에서 표준화 함. CIE RGB color space로 정의되어 현재는 거의 모든 Color science의 기반이 됨.
• Primaries 중 하나와 같은 라이트의 단일 wavelength는 R, G, B primaries를 조합하여 정확하게 표한할 수 없습니다. 실제로 color matching function의 red 함수에 음수값이 있는 부분이 존재합니다.
• Primaries의 조합을 통해서 주어진 λ에 해당하는 단색광(monochromatic light)를 만드는 제한사항 컬러 공간의 gamut을 정의합니다.
• SPD가 있으면 아래와 같이 r(λ), g(λ), b(λ) 컬러 매칭 함수를 곱하여 적분하여 SPD에 해당하는 RGB Primaries를 구할 수 있음. (적분 구간은 380-780nm)

그림8. SPD와 CIE RGB color matching function을 사용하여, 이 SPD를 표현하기 위해서 필요한 RGB Primaries의 양을 얻어냄 (출처 : 레퍼런스1)

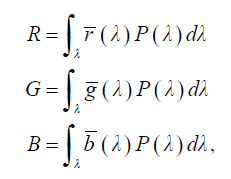
5. The CIE XYZ color space

The CIE RGB Color Space를 국제 표준으로 쓰기에 적절하지 않습니다. 이 이유는 아래와 같습니다.

• 마이너스 값이 존재할 수 있는 것
• 라이트의 luminance (밝기) (색상에 관련없는 인지되어지는 밝기)가 R, G, B 세가지 값을 조합으로 만들어짐

위 단점을 해결하기 위해서 아래와 같은 규칙을 만듭니다.

• 양수 값을 가지는 Tristimulus value 사용
• Tristimulus value 중 하나로 luminance(밝기) 값을 표현

5.1. CIE RGB color space 에서 CIE XYZ color space 로 변환

이런 이유로 CIE XYZ color space가 만들어 졌으며 CIE RGB color space를 선형변환을 하여 생성합니다. 선형변환 시키는 매트릭를 구성할때 아래 2가지를 고려하였습니다.

• r(λ), g(λ), b(λ) 컬러 매칭 함수를 아래 RGB에 넣으면 x(λ), y(λ), z(λ) XYZ 컬러 매칭 함수를 생성할 수 있음
• 매트릭스의 두번째 행은 y(λ)는 luminosity function V(λ)와 가장 유사하게 될 수 있도록 선택됨

그림9. CIE RGB color matching function을 CIE XYZ color matching function으로 변환해주는 매트릭스 (출처 : 레퍼런스1)

X와 Z 요소는 chromaticity(밝기를 무시한 색)에 대응하며 밝기는 고려되지 않았습니다. 이런 요소들은 luminance Y에 의해서 스케일되어 밝아지거나 어두어집니다.

그림10. CIE XYZ color matching function (출처 : 레퍼런스1)

 

 

5.2. Normalized chromaticity coordinates xyz

Normalized chromaticity 좌표 x, y, z는 항상 0~1 사이 값입니다. (x, y, z의 길이가 1이란 뜻임. 각각이 0~1사이가 아님) 이 좌표는 luminance 와 관련 없습니다.

기존의 XYZ 로 부터 x, y, z는 아래의 식을 통해 유도 됩니다.

그림11. XYZ로 부터 normalized chromaticity coordinates xyz를 유도 (출처 : 레퍼런스1)

5.3. xyY color space

xyY는 chromaticity 의 xy만 있으면 z를 유도할 수 있다는 점과 XYZ에서 Y가 Luminance(밝기)를 나타낸다는 점을 사용하여 만들어 졌습니다.

xyY color space는 평균적인 인간 관찰자가 볼 수 있는 모든 색상의 일반적인 표준입니다. 이 컬러 공간을 사용하여 단일 파장이던 여러 파장의 조합이던 상관없이 인간이 볼 수 있는 모든 색상에 대한 정확한 수치를 부여할 수 있습니다. 그래서 xyY는 다른 color space 정의의 기반이 됩니다.

xyY 가 있을때 X와 Z는 아래와 같이 구할 수 있습니다.

그림12. xyY로 부터 XYZ 유도 (출처 : 레퍼런스1)

 

5.4. The CIE xy chromaticity diagram

xy chromaticity 좌표에 대응하는 2차원 컬러 그래프를 CIE xy chromaticity diagram이라 하며, 특징은 아래와 같습니다.

• 인쇄물로 정확히 표현할 할 수 없을 수도 있지만 평균적으로 인간의 눈이 인지할 수 있는 모든 컬러는 포함됨
• 다이어그램의 외곽선은 spectral locus 라 부르며 monochromatic color(단색)를 나타냄
  • Spectral locus 위의 한점 찾기
    • 단일 파장(single wavelength)에 해당하는 XYZ 컴포넌트를 계산하고 x, y로 변환함.
• Spectral locus 위에 있지 않은 색상은 여러 파장의 조합
  • 가장 짧은 것과 가장 긴 파장는 line of purples로 연결됨 (다이어그램 하단)
  • 이 line에 있는 색들은 단일 파장로는 표현할 수 없는 채도가 가장 높은 보라색(fully saturated shades of purple) 을 모두 포함함.
• 다이어그램에서 색상이 있는 영영 바깥은 물리적인 표현이 없기 때문임 imaginary color라고 부름.

그림13. The CIE xy chromaticity diagram (출처 : 레퍼런스1)

5.5. illuminant D65 흰색의 정의

x(λ), y(λ), z(λ) XYZ 컬러 매칭 함수는 모든 가시파장(visible wavelength)에서 동일한 power를 가진 flat 광원을 적분했을때 결과인 XYZ의 요소가 모두 같은 값을 가지도록 정규화되어 있습니다.

이상적인 광원이 X=Y=Z이면, 완벽하게 하얀 라이트는 xy chromaticity coordinates에서 (1/3, 1/3) 입니다. flat SPD는 실제로 매일 나타나지 않기 때문에 CIE 는 standard illuminants를 정의하게됩니다. 이것을 illuminant D65 라 부름. SPD는 그림14에 있음. illuminant D65는 넓은 영역의 촬영지에서 낮의 연평균 값을 근사한 것입니다.

 

그림14. 넓은 영역의 촬영지에서 낮의 연평균 값을 근사한 illuminant D64 (출처 : 레퍼런스1)

 

x(λ), y(λ), z(λ) XYZ 컬러 매칭 함수와 illuminant D65 를 곱하여 적분하면 chromaticity coordinates (xw, yw)를 구할 수 있습니다. 이 xw, yw가 white point 임. 그림13에 중앙에 있는 점입니다.

그림15. illuminant D65 를 통해 얻어낸 chromaticity diagram 상의 좌표 normalized chromaticity coordinates x, y (출처 : 레퍼런스1)

Luminance는 동일한 비율의 Primaries의 혼합시 luminance Yw=1에서 white point의 chromaticity를 생성하도록 정의합니다. illuminant D65 를 통해 정의된 흰색을 xyY 좌표로 표현하면 (xw, yw, Y) = (0.3127, 0.3290, 1) 입니다.

 

6. The sRGB color space

1990s에 디스플레이 디바이스를 위해서 red, gree, blue primaries chromaticities 만듭니다. 이것은 standard RGB color space라 하며, 줄여서 sRGB라 합니다. 주의할 점은 CIE RGB color space와는 다른 것이고, sRGB 의 primaries는 CIE XYZ color space에서 chromaticities의 측면에서 정의되어집니다. 대부분의 컴퓨터 그래픽스 어플리케이션에서 기본으로 사용되는 color space입니다.

6.1. sRGB color space 의 Primaries

sRGB primaries의 chromaticity coordinates는 아래와 같습니다.

• R,G,B primaries는 그림13 처럼 삼각형을 이루는데 이것을 sRGB color space의 color gamut 이라 함.
• 이 삼각형 안의 색상만 디바이스에서 표현 할 수 있으며, 양수에 대해서만 표현가능 함.
• 왼쪽 상단의 많은 영역이 gamut 에서 제외되어있는데, 이 많은 영역의 인지가능한 색상차이가 다른 영역에서는 적은 영역에 대한 색상 차이와 일치함.
  • 그래서 제외된 영역이 많아보이지만 gamut의 적용범위가 나쁘진 않음.

그림16. sRGB primaries 의 chromaticity 좌표 (출처 : 레퍼런스1)

sRGB color space의 white는 위에서 본 그림15의 xw, yw (0.3127, 0.3290)으로 정의됩니다.

6.1.1. sRGB Primaries의 Luminance Y 구하기

이제 이 gamut의 RGB primaries를 가지고 luminance Y를 구해봅시다. xyY를 바로 더할 수 없으므로, RGB primaries 와 white point의 XYZ를 사용하여 Y를 얻어낼 것입니다.

세가지를 모두 더하면 아래와 같은 white point가 나와야 합니다. 그리고 이때의 밝기(Luminance)는 1이 됩니다.

xyY 좌표를 바로 더할 순 없기 때문에 이들의 X,Y,Z 좌표를 더 해야 합니다. 이런 변환은 그림12의 식을 사용해서 아래의 그림17의 식을 유도합니다.

• 식의 좌측항
  • white point 의 xyY 좌표를 사용하여 XYZ 좌표를 구하여 적어줍니다. white point의 luminance (Yw=1)이 었으므로, Y에는 1을 써줍니다.
• 식의 우측항
  • Yw는 RGB Primaries의 밝기의 합일 것이므로, Yr, Yg, Yb 가 그대로 더해질 수 있도록 식을 구성합니다.
  • 그림12의 식을 이용하여 RGB Primaries의 X, Z가 구성될 수 있게 식을 만들어 줍니다. (Yr, Yg, Yb 만 곱해주면 그림12의 식이 완성되도록 매트릭스를 구성)
  • zr, zg, zb는 (1-xr-yr), (1-xg-yg), (1-xb-yb) 임.

그림17. Yr, Yg, Yb 를 얻기 위해 유도한 식 (출처 : 레퍼런스1)

위 방정식을 풀면 RGB Primaries의 밝기 Yr, Yg, Yb 를 얻을 수 있습니다. 실제구현은 7.3장에서 볼 수 있습니다.

그림18. sRGB color space Primaries 들의 Luminance

이제 RGB Primaries 의 luminance 인 Y를 구했으므로 RGB Primaries의 XYZ color space가 완성되었습니다. 그리고 또한 xy역시 알고 있고, 이제 Y를 구했으므로 xyY color space 또한 완성하였습니다.

6.2. XYZ color space 를 sRGB color space로 변환

아래 그림19의 식 우측은 sRGB color space에서 red, green, blue 모두 최대 밝기인 경우입니다. (즉, 하얀색.)

식의 좌측의 각 열은 XYZ 좌표에 해당합니다. xyY로 XYZ를 유도하는 식이 좌측항 입니다. 이 좌표는 sRGB color space의 gamut을 구성하는 primaries와 바로 위에서 얻은 luminance Yr, Yg, Yb를 얻어낸 XYZ 입니다.

그림19. XYZ color space를 sRGB color space로 변환하는 식. 우측항의 RGB에 해당하는 요소가 모두 1이기 때문에 좌측항에 white point의 XYZ 값을 넣어주면 됨. 이 식을 통해서 Msrgb 매트릭스를 유도함. (출처 : 레퍼런스1)

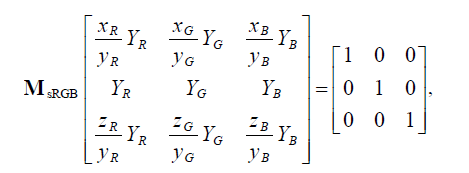
이 식을 정리하면 그림20의 매트릭스를 얻을 수 있습니다. 실제구현은 7.5장에서 볼 수 있습니다.

그림20. XYZ color space 를 sRGB color space로 변환하는 매트릭스 (출처 : 레퍼런스1)

당연하지만 이 매트릭스를 이용해서 D65 white point (sRGB) 를 적용하면 1, 1, 1의 결과가 나옵니다. 실제구현은 7.6장에서 볼 수 있습니다.

그림21. sRGB 변환 매트릭스가 정상 작동하는지 검사 (출처 : 레퍼런스1)

 

6.3. sRGB color space를 XYZ color space로 변환 그리고 sRGB 컬러로 부터 luminance 얻기

간단히 그림20 행렬의 역행렬을 구하면 역변환을 얻을 수 있습니다. 실제구현은 7.4장에서 볼 수 있습니다.

그림22. sRGB color space를 XYZ color space로 변환하는 매트릭스 (출처 : 레퍼런스1)

XYZ color space에서 Y는 luminance를 나타내므로 M srgb inverse 의 두번째 행은 sRGB 컬러의 luminance를 구하는 계수가 됩니다. 아래의 그림23 식을 통해서 이미지를 grayscale로 변환할 수 있습니다.

그림23. sRGB 로 부터 밝기(Luminance)를 구해내는 식

이 식의 계수의 합은 XYZ color space 의 밝기를 나타내는 Y의 최대값인 1입니다. (그림 10 참고). 왜냐하면 하얀색인 경우 sRGB color space에서 RGB는 1, 1, 1이기 때문에 RGB 를 무시할 수 있고, 각 RGB의 계수의 합이 1이 됩니다. 

 

그라스만 법칙에 의해서 sRGB 컬러를 서로 더하거나 곱하는것이 유효하다고 합니다. (이 부분은 잘 알지 못해서 추가로 알아봐야 할 것 같습니다.)

sRGB color 가 표면에서 반사하는 것을 나타내는데 단순히 컴포넌트 요소를 각각 곱하면 되며, 이는 물리적 현실성에 허용가능한 근사치라고 합니다. 컬러 두개를 곱하는 것은 일반적으로 바르지 않지만 추가 정보 없이는 더 나은 결과를 만들 순 없다고 합니다.

SPD를 통해 제대로 계산하게 되면, 라이트로 부터 방출된 SPD는 표면의 Reflection spectrum에 곱해주고, sRGB color space의 컬러 매칭 커브를 곱한 뒤 적분하여 각 컴포넌트의 강도를 결정합니다. 이 강도가 디스플레이에 출력될어질 값이 됩니다. 하지만 게임엔진에서는 계산 비용과 저장공간을 위해서 그냥 단순히 RGB color의 곱셈의 결과를 사용합니다.

7. 실제 연산 테스트

실제 구현 테스트에 사용한 코드는 https://github.com/scahp/Graph/tree/main/ColorScience 에서 찾을 수 있습니다. 파이썬을 통해 구현하였습니다.

• CIE_XYZ_Curve.py 는 CIE_XYZ_Curve 정보와 CIE RGB와 CIE XYZ 변환 매트릭스가 정의 되어있습니다.
• plot.py 는 CIE RGB 또는 CIE XYZ 그래프를 그려줍니다.
• chromaticity.py 는 계산에 필요한 테스트가 담겨있습니다.

7.1. CIE XYZ color matching function 그려보기

• 책 PBRT 의 XX 에서 CIE_X 컬러 매칭 함수를 제공합니다. 이 컬러매칭 함수는 1nm 당 1번씩 샘플링된 결과이며 360 nm to 830 nm 의 데이터가 있습니다. (총 471개 데이터)
• 아래와 같은 형식으로 데이터를 제공합니다.

# CIE_XYZ_Curve.py
...
CIE_X = [
    # CIE X function values
    0.0001299000,   0.0001458470,   0.0001638021,   0.0001840037,
    0.0002066902,   0.0002321000,   0.0002607280,   0.0002930750,
    0.0003293880,   0.0003699140,   0.0004149000,   0.0004641587,
...
CIE_Y = [
    # CIE Y function values
    0.000003917000,  0.000004393581,  0.000004929604,  0.000005532136,
    0.000006208245,  0.000006965000,  0.000007813219,  0.000008767336,
    0.000009839844,  0.00001104323,   0.00001239000,   0.00001388641,

CIE_Z = [
    # CIE Z function values
    0.0006061000,
    0.0006808792,
    0.0007651456,

Python으로 그래프를 그려보면 그림10와 같은 형태의 그래프가 그려집니다.

# plot.py
...
def DrawCIE_XYZ_Curve():
    SetWaveLengthGraph()
    plt.title('CIE XYZ color matching function(CIE XYZ Curve)')
    plt.plot(CIE_XYZ_Curve.RangeWavelength, CIE_XYZ_Curve.CIE_X, 'r', label='X')
    plt.plot(CIE_XYZ_Curve.RangeWavelength, CIE_XYZ_Curve.CIE_Y, 'g', label='Y')
    plt.plot(CIE_XYZ_Curve.RangeWavelength, CIE_XYZ_Curve.CIE_Z, 'b', label='Z')
    plt.legend()
    plt.show()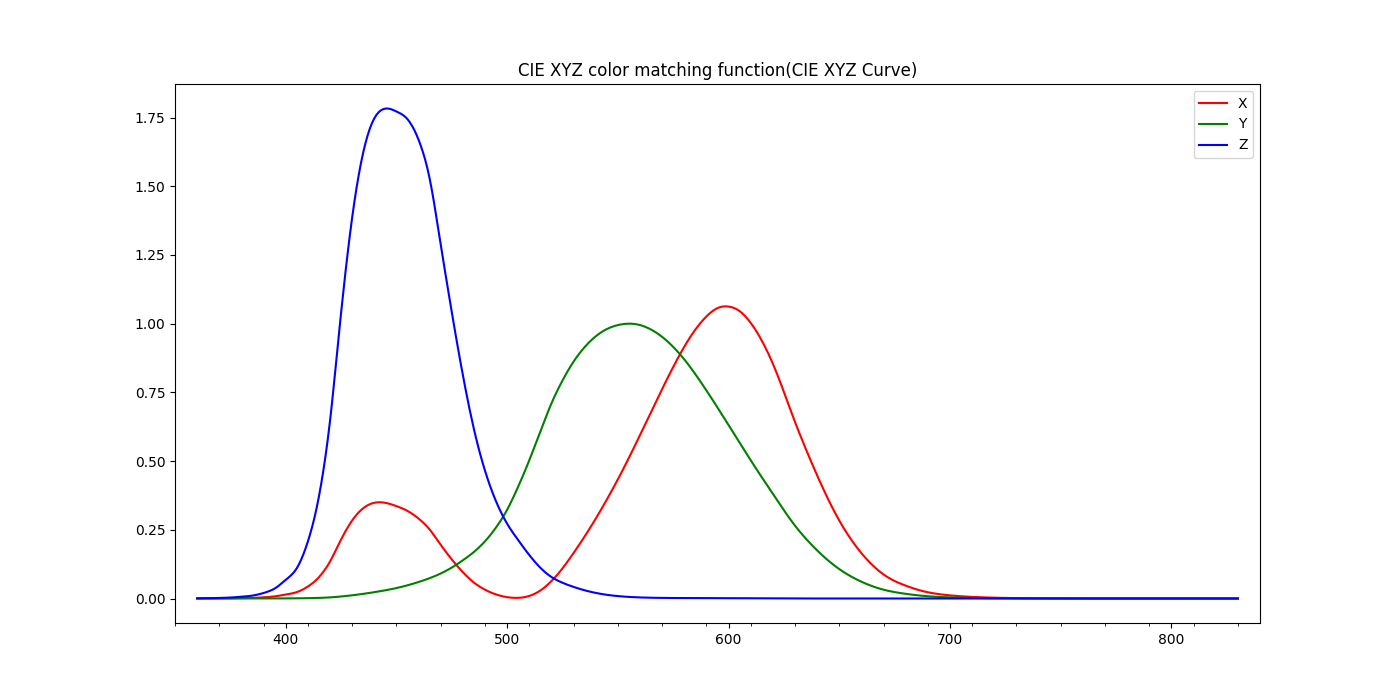

그림22. CIE XYZ color matching function (출처 : 직접구현)

7.2. CIE XYZ color matching function으로 CIE_RGB color matching function 생성하고 그려보기

7.1장에서 사용한 데이터 사용하여 CIE XYZ 를 CIE RGB 컬러 매칭 함수로 변환 시켜봅니다. 그림9에 있는 식의 역변환을 사용하여 변환할 수 있습니다.

# CIE_XYZ_Curve.py
# CIE RGB <-> CIE XYZ linear transform matrix
matCIE_RGB_TO_XYZ = np.array([
          [2.768892, 1.751748, 1.130160],
          [1, 4.590700, 0.060100],
          [0, 0.056508, 5.594292]])
matXYZ_TO_CIE_RGB = np.linalg.inv(matCIE_RGB_TO_XYZ)

...

# plot.py
def DrawCIE_RGB_Curve():
    SetWaveLengthGraph()
    CIE_RGB_X = np.zeros(CIE_XYZ_Curve.NumOfWavelengths)
    CIE_RGB_Z = np.zeros(CIE_XYZ_Curve.NumOfWavelengths)
    CIE_RGB_Y = np.zeros(CIE_XYZ_Curve.NumOfWavelengths)
    # convert from CIE XYZ color matching function to CIE RGB color matching function
    for i in range(0, CIE_XYZ_Curve.NumOfWavelengths):
        CIE_RGB = np.matmul(CIE_XYZ_Curve.matXYZ_TO_CIE_RGB
            , [CIE_XYZ_Curve.CIE_X[i], CIE_XYZ_Curve.CIE_Y[i], CIE_XYZ_Curve.CIE_Z[i]])
        CIE_RGB_X[i] = CIE_RGB[0]
        CIE_RGB_Y[i] = CIE_RGB[1]
        CIE_RGB_Z[i] = CIE_RGB[2]
    plt.title('CIE RGB color matching function(CIE RGB Curve)');
    plt.plot(CIE_XYZ_Curve.RangeWavelength, CIE_RGB_X, 'r', label='R')
    plt.plot(CIE_XYZ_Curve.RangeWavelength, CIE_RGB_Y, 'g', label='G')
    plt.plot(CIE_XYZ_Curve.RangeWavelength, CIE_RGB_Z, 'b', label='B')
    plt.legend()
    plt.show()

 

그림23. CIE RGB color matching function (출처 : 직접구현)

7.3. sRGB Primaries의 luminance 구하기

그림17의 식을 사용하여 sRGB Primaries들의 Luminance Y를 구합니다.

# chromaticity.py
...
# sRGB Primaries which make a gamut in chromaticity diagram
sRGB_Primary_R = [0.64, 0.33]
sRGB_Primary_G = [0.30, 0.60]
sRGB_Primary_B = [0.15, 0.06]


# Chromaticity coordinate of white by using illuminant D65
xw = 0.3127
yw = 0.3290
Yw = 1

# white point of XYZ color space
WhitePoint_XYZ = [xw / yw, Yw, (1.0 - xw - yw) / yw]

def GetLuminance_From_sRGB_Primaries_with_white_of_XYZ():
    a = np.array([
          [sRGB_Primary_R[0]/sRGB_Primary_R[1], sRGB_Primary_G[0]/sRGB_Primary_G[1], sRGB_Primary_B[0]/sRGB_Primary_B[1]],
          [1, 1, 1],
          [(1.0-sRGB_Primary_R[0]-sRGB_Primary_R[1])/sRGB_Primary_R[1], (1.0-sRGB_Primary_G[0]-sRGB_Primary_G[1])/sRGB_Primary_G[1], (1.0 - sRGB_Primary_B[0] - sRGB_Primary_B[1])/sRGB_Primary_B[1]]])
    inva = np.linalg.inv(a);
    Y = np.matmul(inva, WhitePoint_XYZ)
    return Y

print('[Yr, Yg, Yb] : {0}'.format(GetLuminance_From_sRGB_Primaries_with_white_of_XYZ()))

......
결과 : [Yr, Yg, Yb] : [0.21263901 0.71516868 0.07219232]

 

7.4. sRGB 에서 XYZ color space 변환 매트릭스 구성

위에서 구한 sRGB Primaries의 Luminance Y 를 사용하여 컬러 공간 변환 매트릭스를 구성합니다.

# sRGB Primaries which make a gamut in chromaticity diagram
sRGB_Primary_R = [0.64, 0.33]
sRGB_Primary_G = [0.30, 0.60]
sRGB_Primary_B = [0.15, 0.06]

def GetMatrix_sRGB_to_XYZ():
    Y = GetLuminance_From_sRGB_Primaries_with_white_of_XYZ()
    sRGB_to_XYZ = np.array([
                    [sRGB_Primary_R[0]/sRGB_Primary_R[1]*Y[0], sRGB_Primary_G[0]/sRGB_Primary_G[1]*Y[1], sRGB_Primary_B[0]/sRGB_Primary_B[1]*Y[2]],
                    [Y[0], Y[1], Y[2]],
                    [(1.0-sRGB_Primary_R[0]-sRGB_Primary_R[1])/sRGB_Primary_R[1]*Y[0], (1.0-sRGB_Primary_G[0]-sRGB_Primary_G[1])/sRGB_Primary_G[1]*Y[1], (1.0-sRGB_Primary_B[0]-sRGB_Primary_B[1])/sRGB_Primary_B[1]*Y[2]],
                ])
    return sRGB_to_XYZ

...

print('[sRGB to XYZ] : \n{0}'.format(GetMatrix_sRGB_to_XYZ()))

......
결과: 
[sRGB to XYZ] : 
[0.4123908  0.35758434 0.18048079]
[0.21263901 0.71516868 0.07219232]
[0.01933082 0.11919478 0.95053215]

7.5. XYZ 에서 sRGB color space 변환 매트릭스 구성

sRGB 에서 XYZ color space 변환 매트릭스의 역변환 매트릭스로 쉽게 얻을 수 있습니다.

def GetMatrix_XYZ_to_sRGB():
    sRGB_to_XYZ = GetMatrix_sRGB_to_XYZ()
    XYZ_to_sRGB = np.linalg.inv(sRGB_to_XYZ)
    return XYZ_to_sRGB

print('[XYZ to sRGB] : \n{0}'.format(GetMatrix_XYZ_to_sRGB()))

......
결과:
[XYZ to sRGB] : 
[ 3.24096994 -1.53738318 -0.49861076]
[-0.96924364  1.8759675   0.04155506]
[ 0.05563008 -0.20397696  1.05697151]

 

7.6. XYZ 에서 sRGB color space 변환 매트릭스 테스트

흰색 XYZ 를 'XYZ 에서 sRGB color space'로 변환시키는 매트릭스를 사용하여 변환하면 sRGB 값으로 1, 1, 1 나와야 합니다.

whitepoint_sRGB = np.matmul(GetMatrix_XYZ_to_sRGB(), WhitePoint_XYZ);
print('[White point of sRGB] : {0}'.format(whitepoint_sRGB))

결과: [White point of sRGB] : [1. 1. 1.]

8. References

1. Foundations of game engine development 2

2. Electromagnetic Spectrum

3. A Beginner’s Guide to (CIE) Colorimetry

4. Physically Based Rendering:From Theory To Implementation