Atmospheric Shadowing

Atmospheric Shadowing

 

최초 작성 : 2021-04-14

마지막 수정 : 2021-04-14

최재호

 

목차

1. 목표
2. 내용

  2.1 책(FGED2)에 소개된 알고리즘 분석

    2.1.1. Ray marching 할 두 지점 구하기
    2.1.2. Ray marching 시 이동하는 거리(Step)을 점점 더 커지도록 설정
    2.1.3. 랜덤샘플로 성능 향상
    2.1.4. Anistropy scattering
3. 실제 구현
4. 구현 결과
5. 실제 구현 코드
6. 레퍼런스

 

 

1. 목표

Atmospheric Shadowing 을 이해하고 실제로 구현해봅니다.

이글은 VolumeLight 글과 같은 내용을 다루되 레퍼런스1의 Atmospheric Shadowing 챕터를 참고하여 구현하였습니다.

 

2. 내용

알고리즘의 핵심은 간단합니다. 두 지점 (카메라에서 대상 지점까지) 사이를 조금씩 이동하며, 현재 위치에서 Light가 들어오는지 여부를 판단합니다. 만약 Light가 들어오면 Inscattering 되는 구간이라 판단하고 지정한 Inscattering에 수치를 더해줍니다. Light가 현재 위치에 들어오는지 여부는 Depth & Shadow Buffer를 사용합니다. (InScattering 에 대해서는

Absorption and Scattering 를 참고해주세요)

이렇게 지점 A에서 B까지 이동하며 특정 연산을 반복적인 수행하는 것을 Ray marching 이라 부릅니다.. (레퍼런스2 참고)

그리고 이 모든 과정은 PostProcess 과정에서 처리 됩니다.

 

2.1 책(FGED2)에 소개된 알고리즘 분석

2.1.1. Ray marching 할 두 지점 구하기

  2.1.1.1. NDC 공간에서 카메라 공간으로 공간변환

    - NDC 공간의 좌표 v, 초점거리 g 그리고 종횡비 s가 있으면, 카메라 좌표 q를 구할 수 있습니다. 아래의 식1을 봐주세요.

 

식1 : NDC <-> 카메라 공간 변환 (출처 : 직접 작성)

 

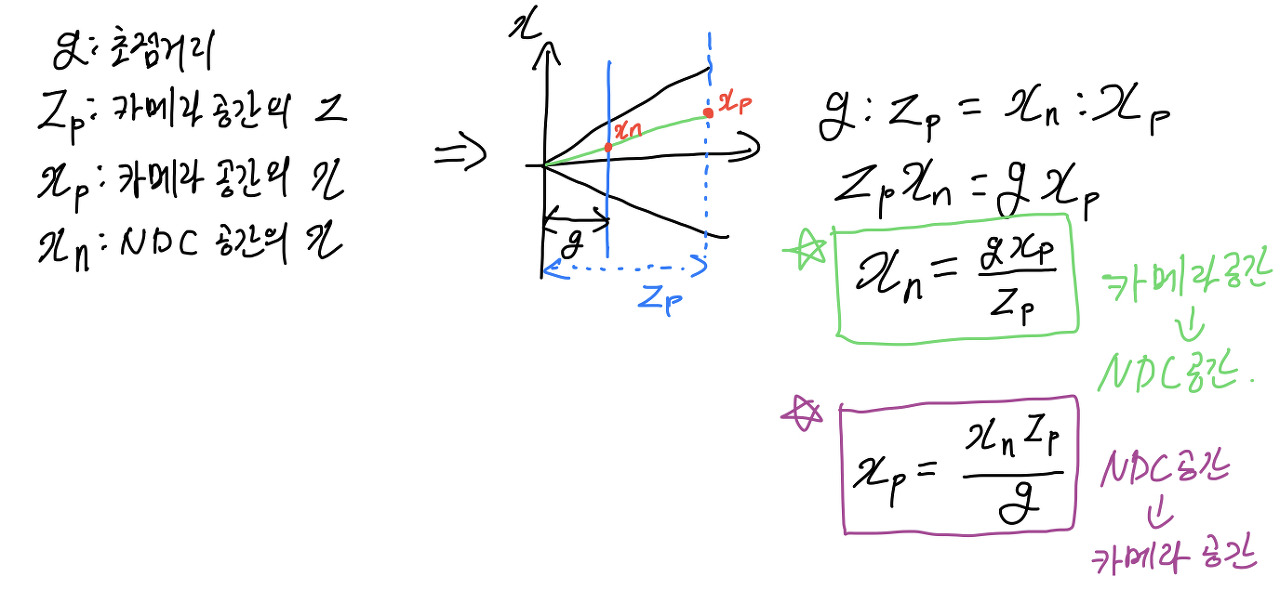
    - 카메라 공간의 좌표는 카메라가 원점에 위치하기 때문에 카메라 원점에서 대상 표면으로의 벡터로 볼 수 있습니다.

 

  2.1.1.2. 쉐도우 텍스쳐로 공간변환

    - 카메라 공간의 좌표에 ShadowMap 용 Projection matrix를 곱해 주어 카메라 공간의 벡터를 ShadowMap에서의 벡터로 변환시켜 줍니다. (ShadowMatrix * (InvViewMat * PositionInCameraSpace))

 

  2.1.1.3. 카메라 원점도 쉐도우 텍스쳐에서 위치를 구함

    - 카메라의 원점에서 부터 벡터방향으로 이동해야 하므로 Camera의 위치 또한 ShadowMap에서의 위치로 변환시켜줍니다.

 

  2.1.1.4. 위의 과정에서 나온 카메라 위치와 벡터를 사용하여 ShadowMap에서 Ray marching을 진행

 

  2.1.1.5. Ray marching 할 시작점과 끝점을 p1, p2로 지정

    - 카메라 위치와 초점거리에 있는 평면사이의 거리로 나눠주어 거리를 |q|와 dmin와 dmax 를 사용하여 p1, p2를 구합니다.

 

식2. 카메라의 방향이 변경되어도 균일한 p1, p2가 동일한 거리를 가질 수있도록 해주는 식 (출처 : 레퍼런스1)

 

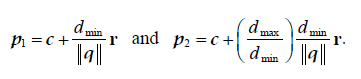
    - 이렇게 식을 구해두면 방향에 상관없이 dmin, dmax 거리를 가진 Radial distance 인 p1와 p2를 얻을 수 있습니다.

    - p1과 p2는 t를 0-1 까지로 변화시키며 보간할 수 있습니다.

    - ShadowMap에서는 좌표는 xy축만 있으며, 이 x, y에 대응하는 z값 또한 구해야 합니다. 이 역시 동일하게 방식으로 보간하여 구할 수 있스빈다. 식3 참고.

 

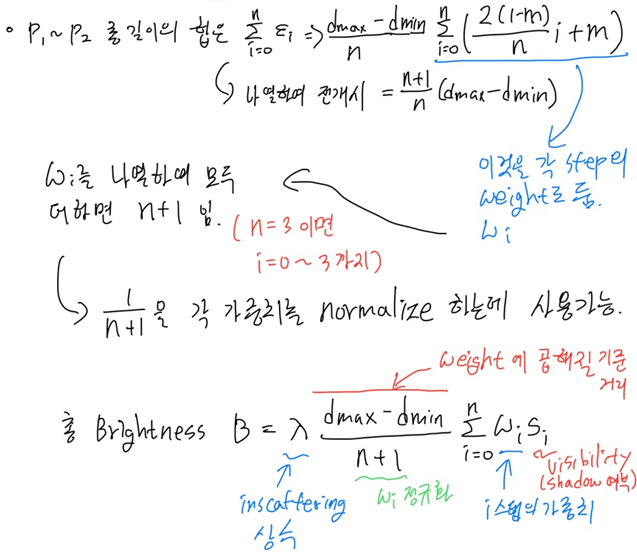
2.1.2. Ray marching 시 이동하는 거리(Step)을 점점 더 커지도록 설정

  - 현재 위치에서 더 멀리 있을 수록 쉐도우맵에서의 비지빌리티 밀도가 떨어집니다. 오버샘플링을 줄이기 위해서 카메라에서 멀어질 수록 Step을 증가시킵니다.

  - 이 식은 복잡하지만 정확하게 밀도에 비례하는 Step을 조정하는 식은 아닙니다. 그래서 큰차이가 없는 경우는 고정 Step 이동을 하는 것도 괜찮다고 생각합니다.

  - u(t) 함수를 정의하여서 이런 작업을 수행합니다. 아래의 총 Brightness 식 유도를 참고해주세요.

 

 

그림1. u(t) 함수 유도1 (출처 : 직접 작성)

그림2. u(t) 함수 유도2 (출처 : 직접 작성)

식3. 최종 Brightness 식 (출처 : 레퍼런스1)

 

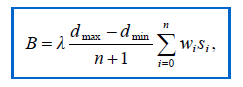
2.1.3. 랜덤샘플로 성능 향상

  - t = i / n을 t = (i + delta) / n 으로 설정 delta는 노이즈 64x64 텍스쳐에서 가져옵니다.

  - 이웃 픽셀을 갖고 블러를 해도 되지만 그렇게되면 배경의 light shaft가 전경의 솔리드 오브젝트로 번지는 라이트 블리딩 현상이 발생가능합니다.

 

2.1.4. Anistropy scattering

  2.1.4.1. 디렉셔널 라이트의 성질

    - 대기에서 디렉셔널 라이트는 등방성 산란을 하지 않습니다, 대부분은 라이트의 방향 그대로거나 아주 적은 각도만 변하고 뒤쪽이나 큰 각도로 변하는 경우는 적습니다. 그래서 태양을 바라보는 경우는 라이트가 강하지만 태양을 바라보지 않으면 라이트는 아주 적습니다.

  2.1.4.2. 비등방성 성질을 추가하기 위해 식

 

식4. Anisotropy scattering 을 위한 식 : Henyey-Greenstein phase function (출처 : 레퍼런스1)

 

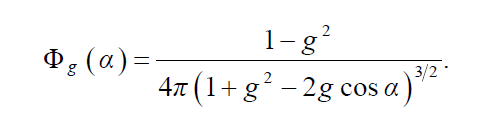
    - α : 카메라에서 표면으로 향하는 방향과 라이트 방향 사이의 각

    - 90보다 적으면 라이트가 앞쪽으로 산란하는 포워드 스케터링 90보다 크면 뒤쪽으로 산란하는 백워드 스케터링입니다. 아래 식을 참고해주세요.

 

식5. Forward, Backward Scattering을 위한 식 (출처 : 레퍼런스1)

 

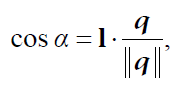
  - g : g가 0 이면 모든 방향으로 균일하게 산란합니다. 그리고 g > 0 이면 입사하는 라이트 방향에 가까운 방향으로 산란하며 g값이 더 클수록 라이트의 방향으로 더 많이 산란합니다.

    - g 항이 계속해서 커지는 경우, 알파 값이 0 일때 가장 큰 값을 생성합니다. 그래서 최대 Intensity는 아래와 같습니다.

 

식6. 최대 Intensity 값을 가지는 식 (출처 : 레퍼런스1)

 

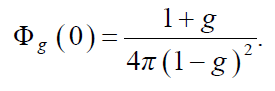
    - 이러한 값의 변화는 level의 anisotropy 값을 변경했을 때 Brightness 또한 변경되므로 원치 않는 결과를 일으킬 수 있음. 그래서 최대값인 Φg(0)을 사용하여 'Φg(알파) 값을 정규화 하여 사용합니다.

 

식7. 정규화 시킨 Henyey-Greenstein phase function (출처 : 레퍼런스1)

 

 

 

그림3. 좌측은 원본, 우측은 정규화시킨 결과. isotropy scattering의 경우(파란색)이 1값으로 정규화되면서 우측 그림에서 가장 큰 영역을 커퍼하게 됨. 정규화하게 되면 실제 물리적으로 옳바른 성질을 잃는다고 볼 수 있음. (출처 : 레퍼런스1)

 

 

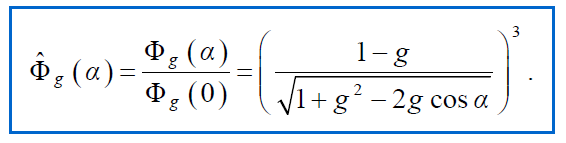
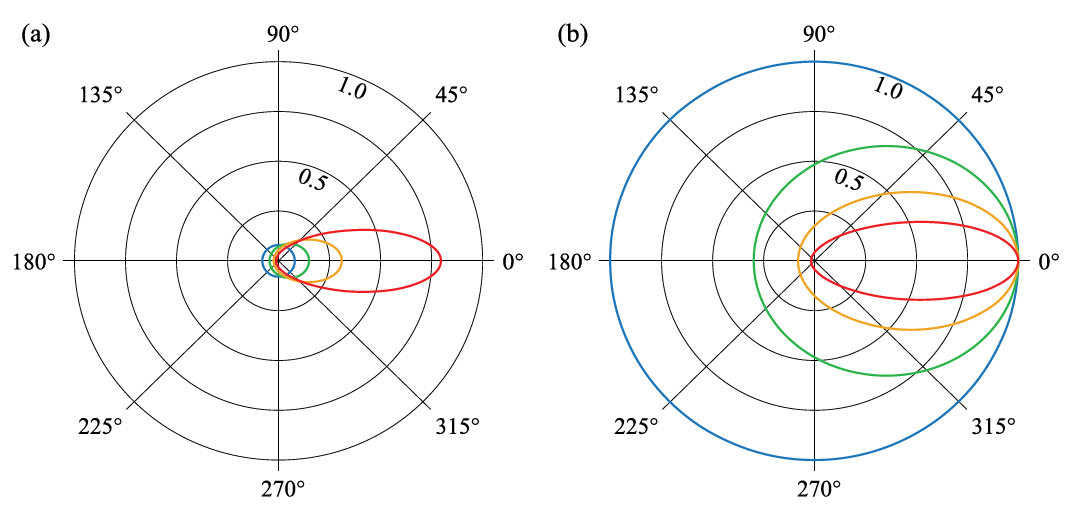
    - g값을 그냥 제공 하는 것 보다 아티스트가 선택한 최소 Intensity R을 통해 g를 만들어내는 것이 더 유용할 수 있습니다.

      - 알파가 180도 인 경우 R이 최소값이 되기 때문에 아래식을 통해 g를 유도합니다.

      - 최대값의 경우 정규화 된 값이 항상 1이므로 사용하기 어렵기 때문에 최소값을 사용함. 최소값은 g가 바뀜에 따라서 값이 달라지므로 Backward scattering과 Forward scattrering의 비율로 볼 수 있습니다.

 

 

식8. 180도에서 가장 적은 값을 가진다. (출처 : 레퍼런스1)

식9. 식8을 사용하여 g를 유도 (출처 : 레퍼런스1)

 

 

 

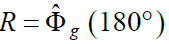
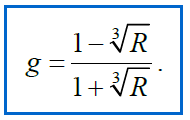
3. 실제 구현

실제 구현은 책에 있는 내용과는 다르게 구현하였습니다.

 

이유는 아래와 같습니다.

책의 구현을 따라갔을 때, ShadowRay(쉐도우 텍스쳐 공간에서의 반직선)에 Camera 공간의 DepthRatio를 곱해주는 부분이 있었고, 이 부분이 dmin = 1.0, dmax=1000 인경우는 p2 값이 너무 큰 값으로 유도되어 (500이상) 쉐도우 텍스쳐 공간에서 Ray marching이 불가능하였기 때문입니다.

 

그림4. 문제가 된다고 생각한 부분 (출처 : 레퍼런스1)

 

 

float GetAccumulatedInscatteringValue(float InTravelDist, vec3 InToPixelNormalized)
{
  float Depth = texture(DepthSampler, TexCoord_).x;

  float dt = 1.0 / TravelCount;
  float dw = 2.0 * (1.0 - SlopeOfDist) * dt;

  float t = dt;
  if (UseNoise != 0)
    t += dt * rand(vec2(gl_FragCoord.x * gl_FragCoord.y / CameraFar)) * 3.0;
  float tmax = t + 1.0;

  // Start and end Depth to march ray in NDC
  float z1 = TransformNDC(CameraPos + InToPixelNormalized * CameraNear).z;
  float z2 = TransformNDC(CameraPos + InToPixelNormalized * InTravelDist).z;

  // Start and end pos in shadowmap texture space
  vec3 p1 = TransformShdowMapTextureSpace(CameraPos + CameraNear);
  vec3 p2 = TransformShdowMapTextureSpace(CameraPos + InToPixelNormalized * InTravelDist);

  float weight = SlopeOfDist;  // first weight is always SlopeOfDist

  float AccumulatedValue = 0.0;
  for (; t <= tmax; t += dt)
  {
    float u = (t * (1.0 - SlopeOfDist) + SlopeOfDist) * t;
    float z = mix(z1, z2, u);

    // When the z meet Depth on screen, stop raymarching
    if (z > Depth)
      break;

    vec3 CurrentPosInShadowMapTS = mix(p1, p2, u);
    float ShadowMapDepth = texture(ShadowMapSampler, CurrentPosInShadowMapTS.xy).x;
    if (ShadowMapDepth > CurrentPosInShadowMapTS.z)
      AccumulatedValue += weight;

    weight += dw;
  }

  return AccumulatedValue;
}

코드1. Raymarching (출처 : 직접 구현)

 

원본 알고리즘과 다른 점은 아래 3가지 입니다.

- Noise 텍스쳐 대신 rand 함수를 만들어 적용

- ShadowMapTS 공간에서 Raymarching할 p1, p2를 구하고 보간하여 사용

- NDC 공간에서 Raymarching할 z1, z2를 구하고 보간하여 사용

 

float AnisotropyIntensity(vec3 InFromSurfaceToCamera)
{
  float atmosphereBrightness = InScatteringLambda * (CameraFar - CameraNear) / TravelCount; // lambda * (dmax − dmin) / (n + 1)

  float g = AnisoG;
  vec3 anisotropyConst = vec3(1.0 - g, 1.0 + g * g, 2.0 * g); // (1 − g, 1 + g * g, 2 * g)

  float invLength = 1.0;
  float h = anisotropyConst.x * (1.0 / sqrt(anisotropyConst.y - anisotropyConst.z * dot(InFromSurfaceToCamera, LightCameraDirection)));
  float intensity = h * h * h * atmosphereBrightness;

  return intensity;
}

코드2. Anisotropy scattering (출처 : 직접 구현)

 

 

4. 구현 결과

 

그림5. 구현결과 (출처 :직접 구현)

그림6. 구현결과 (출처 :직접 구현)

그림7. 구현결과 Anisotropy scattering (출처 :직접 구현)

그림8. Raymarching 40 Step 인 상황에서 Noise 끄기 (출처 :직접 구현)

 

그림9. 그림8에서 Noise 켜기 (출처 :직접 구현)

 

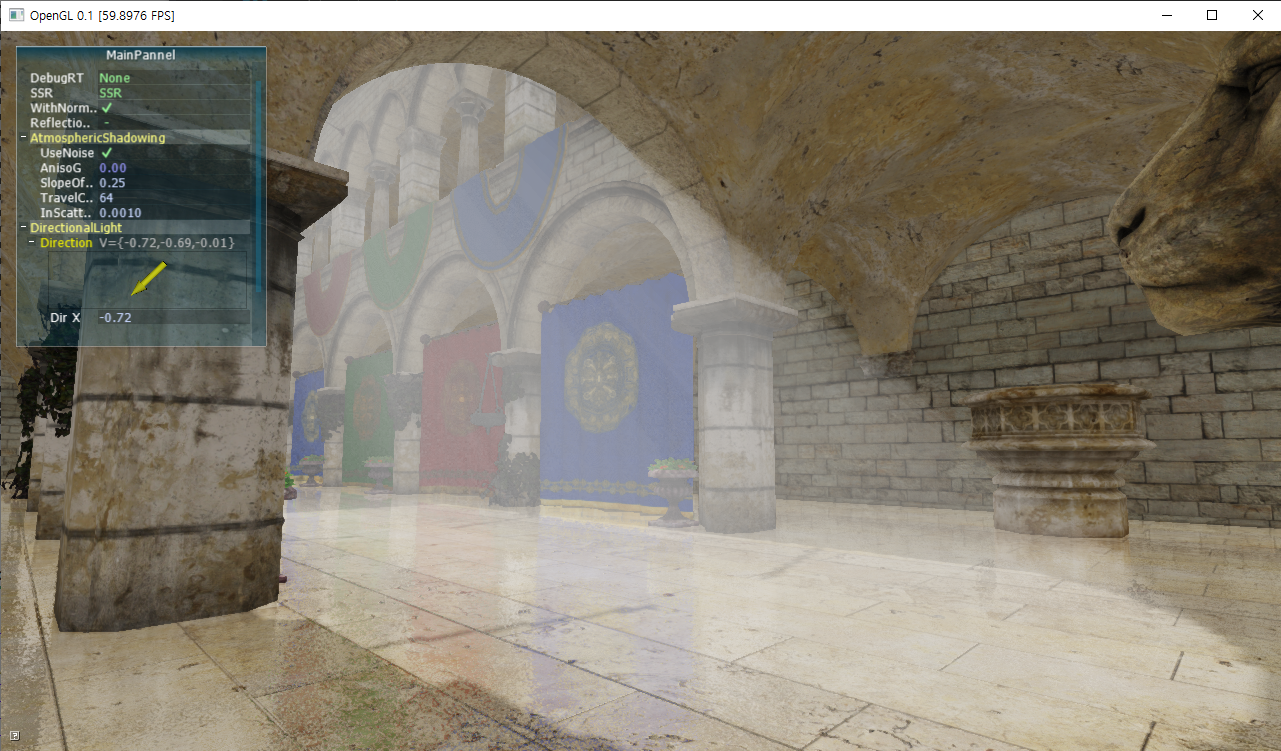
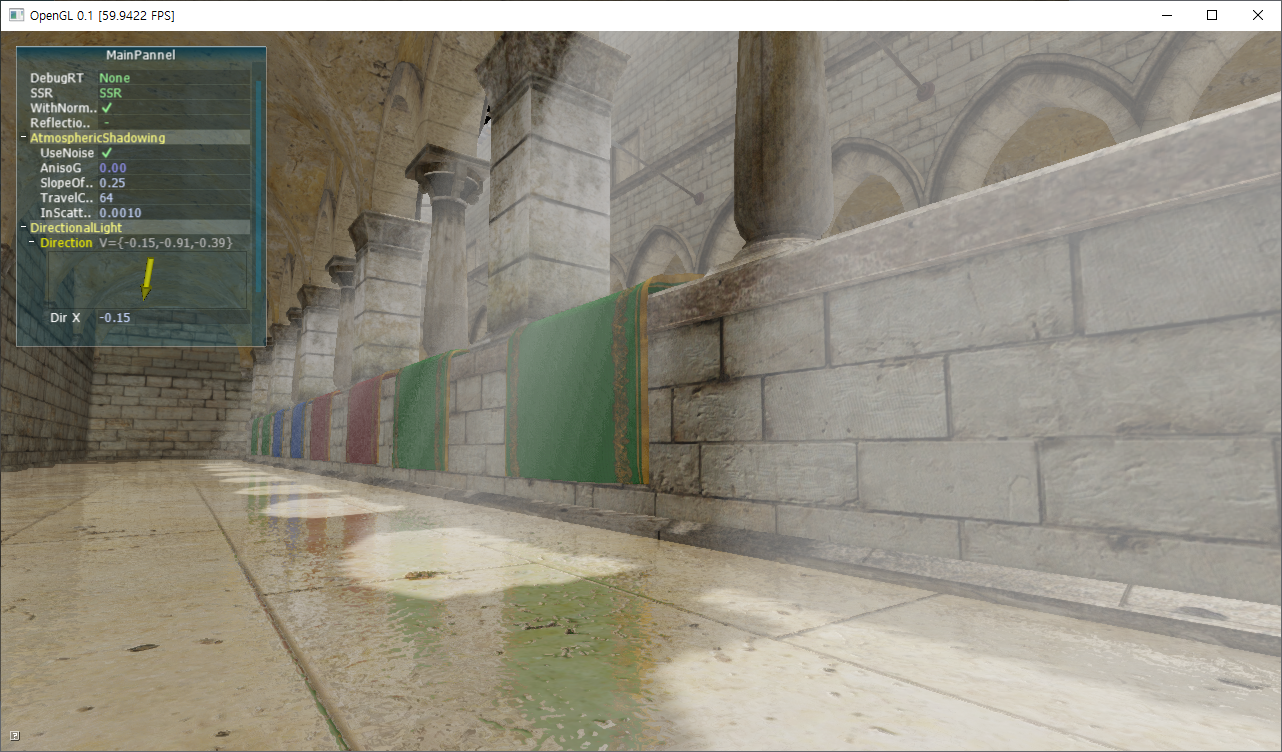
5. 실제 구현 코드

github.com/scahp/Shadows/tree/sponza_atmosphericshadowing

 

6. 레퍼런스

1. Foundations of Game Engine Development, Volume 2: Rendering

2. computergraphics.stackexchange.com/questions/161/what-is-ray-marching-is-sphere-tracing-the-same-thing/163